
| A. | 3 | B. | 2 | C. | $\sqrt{2}$ | D. | 1 |
分析 在一个棱长为6的正四面体纸盒内放一个正方体,并且能使正方体在纸盒内任意转动,说明正方体在正四面体的内切球内,求出内切球的直径,就是正方体的对角线的长,然后求出正方体的棱长.
解答 解:设球的半径为r,由正四面体的体积得:
$4×\frac{1}{3}×r×{6}^{2}$=$\frac{1}{3}×\frac{\sqrt{3}}{4}×{6}^{2}×\sqrt{{6}^{2}-(\frac{2}{3}×\frac{\sqrt{3}}{2}×6)^{2}}$,
解得r=$\frac{\sqrt{6}}{2}$,
设正方体的最大棱长为a,
∴3a2=($\sqrt{6}$)2,解得a=$\sqrt{2}$.
故选:C.
点评 本题是中档题,考查正四面体的内接球的知识,球的内接正方体的棱长的求法,考查空间想象能力,转化思想,计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{1}{64},1]$ | B. | $[\frac{1}{8},1]$ | C. | $(\frac{1}{64},1)$ | D. | $(\frac{1}{8},1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED是以BD为直角腰的直角梯形,DE=2BF=2,平面BFED⊥平面ABCD.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED是以BD为直角腰的直角梯形,DE=2BF=2,平面BFED⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
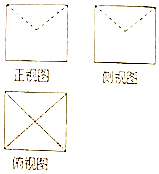 某几何体的三视图如图所示,图中的四边形都是边长为1的正方体,两条虚线互相垂直,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为1的正方体,两条虚线互相垂直,则该几何体的体积是( )| A. | $\frac{2}{3}$ | B. | $\frac{5}{6}$ | C. | $1-\frac{π}{6}$ | D. | $1-\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com