
【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定80分及以上者晋级成功,否则晋级失败(满分为100分).


(1)求图中![]() 的值;
的值;
(2)估计该次考试的平均分![]() (同一组中的数据用该组的区间中点值代表);
(同一组中的数据用该组的区间中点值代表);
(3)根据已知条件完成下面![]() 列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
(参考公式:  ,其中
,其中![]() )
)
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) ![]() 分;(Ⅲ)见解析.
分;(Ⅲ)见解析.
【解析】试题分析:(1)根据频率分布直方图矩形面积和为1可求出![]() ;
;
(2)根据每个小矩形的中点乘以面积求和即可;
(3)套用![]() 的计算公式求值,查表下结论即可.
的计算公式求值,查表下结论即可.
试题解析:
(Ⅰ)由频率分布直方图各小长方形面积总和为1,可知
![]() ,故
,故![]() .
.
(Ⅱ) 由频率分布直方图知各小组依次是![]() ,
,
其中点分别为![]() 对应的频率分别为
对应的频率分别为![]() ,
,
故可估计平均分
![]() (分)
(分)
(Ⅲ)由频率分布直方图知,晋级成功的频率为![]() ,
,
故晋级成功的人数为![]() (人),故填表如下
(人),故填表如下
晋级成功 | 晋级失败 | 合计 | |
男 | 16 | 34 | 50 |
女 | 9 | 41 | 50 |
合计 | 25 | 75 | 100 |
假设“晋级成功”与性别无关,
根据上表数据代入公式可得![]() ,
,
所以有超过85%的把握认为“晋级成功”与性别有关.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:
【题目】“公益行”是由某公益慈善基金发起并主办的一款将用户的运动数据转化为公益步数的捐助公益项目的产品,捐助规则是满10000步方可捐助且个人捐出10000步等价于捐出1元,现粗略统计该项目中其中200名的捐助情况表如下:
捐款金额(单位:元) |
|
|
|
|
|
|
捐款人数 | 4 | 152 | 26 | 10 | 3 | 5 |
(1)将捐款额在200元以上的人称为“健康大使”,请在现有的“健康大使”中随机抽取2人,求捐款额在![]() 之间人数
之间人数![]() 的分布列;
的分布列;
(2)为鼓励更多的人来参加这项活动,该公司决定对捐款额在100元以上的用户实行红包奖励,具体奖励规则如下:捐款额在![]() 的奖励红包5元;捐款额在
的奖励红包5元;捐款额在![]() 的奖励红包8元;捐款额在
的奖励红包8元;捐款额在![]() 的奖励红包10元;捐款额大于250的奖励红包15元.已知该活动参与人数有40万人,将频率视为概率,试估计该公司要准备的红包总金额.
的奖励红包10元;捐款额大于250的奖励红包15元.已知该活动参与人数有40万人,将频率视为概率,试估计该公司要准备的红包总金额.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ;
;
(1)若函数![]() 在
在![]() 上为增函数,求正实数
上为增函数,求正实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最值;
上的最值;
(3)当![]() 时,对大于1的任意正整数
时,对大于1的任意正整数![]() ,试比较
,试比较![]() 与
与![]() 的大小关系.
的大小关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如图,圆![]() 、椭圆
、椭圆![]() 均经过点M
均经过点M![]() ,圆
,圆![]() 的圆心为
的圆心为![]() ,椭圆
,椭圆![]() 的两焦点分别为
的两焦点分别为![]() .
.

(Ⅰ)分别求圆![]() 和椭圆
和椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过![]() 作直线
作直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,试探究
两点,试探究![]() 是否为定值?若是定值,求出该定值;若不是,说明理由.
是否为定值?若是定值,求出该定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() 的底面为矩形,D为
的底面为矩形,D为![]() 的中点,AC⊥平面BCC1B1.
的中点,AC⊥平面BCC1B1.

(Ⅰ)证明:AB//平面CDB1;
(Ⅱ)若AC=BC=1,BB1=![]() ,
,
(1)求BD的长;
(2)求B1D与平面ABB1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]()
![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,且当倾斜角为
两点,且当倾斜角为![]() 的直线
的直线![]() 经过抛物线
经过抛物线![]() 的焦点
的焦点![]() 时,有
时,有![]() .
.
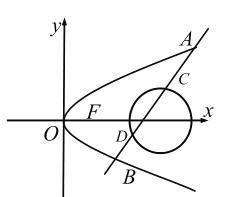
(1)求抛物线![]() 的方程;
的方程;
(2)已知圆![]() ,是否存在倾斜角不为
,是否存在倾斜角不为![]() 的直线
的直线![]() ,使得线段
,使得线段![]() 被圆
被圆![]() 截成三等分?若存在,求出直线
截成三等分?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列函数f(x)中,满足“任意x1 , x2∈(0,+∞),且x1≠x2 , 都有(x1﹣x2)[f(x1)﹣f(x2)]<0”的是( )
A.f(x)= ![]() ﹣x
﹣x
B.f(x)=x3
C.f(x)=ln x
D.f(x)=2x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级随机抽取了![]() 名学生第一学期的数学学期综合成绩和物理学期综合成绩.
名学生第一学期的数学学期综合成绩和物理学期综合成绩.
列表如下:
学生序号 |
|
|
|
|
|
|
|
|
|
|
数学学期综合成绩 |
|
|
|
|
|
|
|
|
|
|
物理学期综合成绩 |
|
|
|
|
|
|
|
|
|
|
学生序号 |
|
|
|
|
|
|
|
|
|
|
数学学期综合成绩 |
|
|
|
|
|
|
|
|
|
|
物理学期综合成绩 |
|
|
|
|
|
|
|
|
|
|
规定:综合成绩不低于![]() 分者为优秀,低于
分者为优秀,低于![]() 分为不优秀.
分为不优秀.
对优秀赋分![]() ,对不优秀赋分
,对不优秀赋分![]() ,从
,从![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生,若用
名学生,若用![]() 表示这
表示这![]() 名学生两科赋分的和,求
名学生两科赋分的和,求![]() 的分布列和数学期望;
的分布列和数学期望;
根据这次抽查数据,列出![]() 列联表,能否在犯错误的概率不超过
列联表,能否在犯错误的概率不超过![]() 的前提下认为物理成绩与数学成绩有关?
的前提下认为物理成绩与数学成绩有关?
附:  ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com