
【题目】已知函数![]() ;
;
(1)若函数![]() 在
在![]() 上为增函数,求正实数
上为增函数,求正实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最值;
上的最值;
(3)当![]() 时,对大于1的任意正整数
时,对大于1的任意正整数![]() ,试比较
,试比较![]() 与
与![]() 的大小关系.
的大小关系.
【答案】(1)![]() ;(2)函数
;(2)函数![]() 在区间
在区间![]() 上的最大值是
上的最大值是![]() ,最小值是0;(3)见解析.
,最小值是0;(3)见解析.
【解析】试题分析:(1)先求出函数的导数,解关于导函数的不等式,求出a的范围即可;
(2)将a=1代入,求出函数的导数,得到函数的单调区间,从而求出函数的最小值;
(3)求出函数的导数,得到函数的单调性,令![]() ,得到f(x)>f(1)=0,从而证出结论.
,得到f(x)>f(1)=0,从而证出结论.
试题解析:(1)因为![]() ,所以
,所以![]()
因为函数![]() 在
在![]() 上为增函数,所以
上为增函数,所以![]() 对
对![]() 恒成立,
恒成立,
所以![]() 对
对![]() 恒成立,即
恒成立,即![]() 对
对![]() 恒成立,所以
恒成立,所以![]() .
.
(2)当![]() 时,
时,![]() ,所以当
,所以当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上单调递减;当
上单调递减;当![]() ,
,![]() ,故
,故![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() 在区间
在区间![]() 上有唯一极小值点,故
上有唯一极小值点,故![]() ,又
,又![]() ,
,![]() ,,
,,![]()
因为![]() ,所以
,所以![]() ,即
,即![]()
所以![]() 在区间
在区间![]() 上的最大值是
上的最大值是![]()
综上可知,函数![]() 在区间
在区间![]() 上的最大值是
上的最大值是![]() ,最小值是0.
,最小值是0.
(3)当![]() 时,
时,![]() ,
,![]() ,故
,故![]() 在
在![]() 上为增函数.
上为增函数.
当![]() 时,令
时,令![]() ,则
,则![]() ,故
,故![]()
所以 ,即
,即![]() >
>![]()
当![]() 时,对大于1的任意正整数
时,对大于1的任意正整数![]() ,有
,有 ![]() >
>![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知一家公司生产某种产品的年固定成本为6万元,每生产1千件需另投入2.9万元,设该公司一年内生产该产品![]() 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为![]() 万元,且
万元,且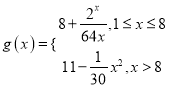 .
.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)求该公司生产这一产品的最大年利润及相应的年产量.(年利润=年销售收入-年总成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,求实数
上单调递增,求实数![]() 的值;
的值;
(2)是否存在实数![]() ,使得
,使得![]() 在
在![]() 上单调递减,若存在,试求
上单调递减,若存在,试求![]() 的取值范围;若不存在,请说明理由;
的取值范围;若不存在,请说明理由;
(3)若![]() ,当
,当![]() 时不等式
时不等式![]() 有解,求实数
有解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了分析某个高三学生的学习状态,对其下一阶段的学习提供指导性建议.现对他前![]() 次考试的数学成绩
次考试的数学成绩![]() 、物理成绩进行分析.下面是该生
、物理成绩进行分析.下面是该生![]() 次考试的成绩.
次考试的成绩.
数学 | 108 | 103 | 137 | 112 | 128 | 120 | 132 |
物理 | 74 | 71 | 88 | 76 | 84 | 81 | 86 |
(Ⅰ)他的数学成绩与物理成绩哪个更稳定?请给出你的说明;
(Ⅱ)已知该生的物理成绩![]() 与数学成绩是线性相关的,求物理成绩
与数学成绩是线性相关的,求物理成绩![]() 与数学成绩的回归直线方程
与数学成绩的回归直线方程
(Ⅲ)若该生的物理成绩达到90分,请你估计他的数学成绩大约是多少?
(附:  )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定80分及以上者晋级成功,否则晋级失败(满分为100分).


(1)求图中![]() 的值;
的值;
(2)估计该次考试的平均分![]() (同一组中的数据用该组的区间中点值代表);
(同一组中的数据用该组的区间中点值代表);
(3)根据已知条件完成下面![]() 列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
(参考公式:  ,其中
,其中![]() )
)
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知☉O:x2+y2=1和定点A(2,1),由☉O外一点P(a,b)向☉O引切线PQ,切点为Q,且满足|PQ|=|PA|.

(1)求实数a,b间满足的等量关系.
(2)求线段PQ长的最小值.
(3)若以P为圆心所作的☉P与☉O有公共点,试求半径取最小值时☉P的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com