
【题目】如图,四棱锥 ![]() 中,底面
中,底面 ![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)证明:平面 ![]() 平面
平面 ![]() ;
;
(Ⅱ)若二面角 ![]() 为
为 ![]() ,求
,求 ![]() 与平面
与平面 ![]() 所成角的正弦值.
所成角的正弦值.
【答案】解:(Ⅰ)∵ ![]() ,
, ![]()

![]() ,
,
![]()
![]()
∴ ![]() ⊥平面
⊥平面 ![]() ,
, ![]()
∴ ![]()
又 ![]()
∴ ![]()
又 ![]()
![]() ,
, ![]()
![]() ,又因为
,又因为 ![]() ∥
∥ ![]()
∴ ![]()
又∵ ![]() ,
, ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]()
∴ ![]() 平面
平面 ![]()
而 ![]() 平面
平面 ![]() ∴平面
∴平面 ![]() 平面
平面 ![]()
(Ⅱ)由(Ⅰ)所证, ![]() 平面
平面 ![]()
所以∠ ![]() 即为二面角
即为二面角 ![]() 的平面角,即∠
的平面角,即∠ ![]()
而 ![]() ,所以
,所以 ![]()
分别以 ![]() 、
、 ![]() 、
、 ![]() 为
为 ![]() 轴、
轴、 ![]() 轴、
轴、 ![]() 轴建立空间直角坐标系。
轴建立空间直角坐标系。
则 ![]() ,
, ![]() ,
, ![]() ,
, ![]()
所以, ![]() ,
, ![]() ,
, ![]()
设平面 ![]() 的法向量为
的法向量为 ![]() ,则
,则 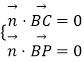
即 ![]() 可取
可取 ![]()
∴ ![]() 与平面
与平面 ![]() 所成角的正弦值为
所成角的正弦值为 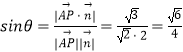
【解析】(I)证明面面垂直,关键是线面垂直,由题知P D ⊥平面 A B C D,可得P D ⊥ B C,,根据余弦定理可得B C ⊥ B D,得证。
(II)由第(I)问可建系,根据长度关系,求出点的坐标,进而求出面OBC的法向量,应用线面角的公式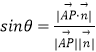 可得。
可得。
【考点精析】认真审题,首先需要了解平面与平面垂直的判定(一个平面过另一个平面的垂线,则这两个平面垂直),还要掌握用空间向量求直线与平面的夹角(设直线![]() 的方向向量为
的方向向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,直线与平面所成的角为
,直线与平面所成的角为![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() , 则
, 则![]() 为
为![]() 的余角或
的余角或![]() 的补角的余角.即有:
的补角的余角.即有: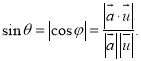 )的相关知识才是答题的关键.
)的相关知识才是答题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】假设你家订了一份报纸,送报人可能在早上6点—8点之间把报纸送到你家,你每天离家去工作的时间在早上7点—9点之间.
问:离家前不能看到报纸(称事件![]() )的概率是多少?(须有过程)
)的概率是多少?(须有过程)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心为
的圆心为![]() ,且截
,且截![]() 轴所得的弦长为
轴所得的弦长为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)设圆![]() 与
与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,过
,过![]() 分别作斜率为
分别作斜率为![]() 的两条直线交圆
的两条直线交圆![]() 于
于![]() 两点,且
两点,且![]() ,试证明直线
,试证明直线![]() 恒过一定点,并求出该定点坐标.
恒过一定点,并求出该定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】利民中学为了了解该校高一年级学生的数学成绩,从高一年级期中考试成绩中抽出100名学生的成绩,由成绩得到如下的频率分布直方图.
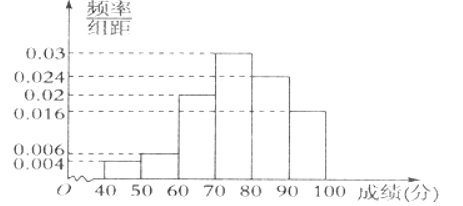
根据以上频率分布直方图,回答下列问题:
(1)求这100名学生成绩的及格率;(大于等于60分为及格)
(2)试比较这100名学生的平均成绩和中位数的大小.(精确到0.1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如右图抛物线顶点在原点,圆(x﹣2)2+y2=22的圆心恰是抛物线的焦点,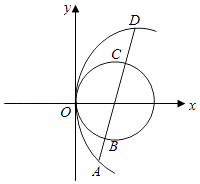
(Ⅰ)求抛物线的方程;
(Ⅱ)一直线的斜率等于2,且过抛物线焦点,它依次截抛物线和圆于A、B、C、D四点,求|AB|+|CD|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com