
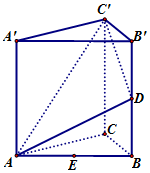
 如图,已知正三棱柱ABC-A'B'C'棱长均为2,E为AB中点.点D在侧棱BB'上.
如图,已知正三棱柱ABC-A'B'C'棱长均为2,E为AB中点.点D在侧棱BB'上.分析 (Ⅰ)将三棱柱的侧面展开,由题意知当D为BB′中点时,AD+DC′最小,由此能求出AD+DC′的最小值.
(Ⅱ)过点E作EM∥AD交BB′于M,M为BD中点,过点M作MF∥DC′交CC′于F,由面MEF∥面ADC′,得EF∥面ADC′.
解答 解:(Ⅰ)如图,将三棱柱的侧面展开,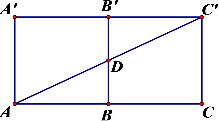
由题意知当D为BB′中点时,AD+DC′最小,
最小值为d=$\sqrt{{4}^{2}+{2}^{2}}=2\sqrt{5}$.(4分)
(Ⅱ)过点E作EM∥AD交BB′于M,所以M为BD中点,(6分)
过点M作MF∥DC′交CC′于F,
∴${C}^{′}F=\frac{1}{2}$,(10分)
∵EM∩MF=M,
∴面MEF∥面ADC′,∴EF∥面ADC′.(12分)
点评 本题考查两线段和的最小值的求法,考查使直线与平面平行的点的位置的确定,空间问题转化为平面问题是解题关键,是中档题.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
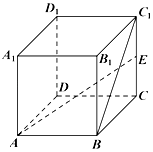 长方体ABCD-A1B1C1D1中AB=AA1=2,AD=1,E为CC1的中点且$AE=\sqrt{6}$,则异面直线BC1与AE所成角的余弦值为( )
长方体ABCD-A1B1C1D1中AB=AA1=2,AD=1,E为CC1的中点且$AE=\sqrt{6}$,则异面直线BC1与AE所成角的余弦值为( )| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{\sqrt{30}}{10}$ | C. | $\frac{2\sqrt{15}}{10}$ | D. | $\frac{3\sqrt{10}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2次 | B. | 3次 | C. | 4次 | D. | 5次 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| X | 0 | 1 | 2 | 3 | 4 |
| P | 0.2 | 0.1 | 0.1 | 0.3 | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | an=4×($\frac{3}{2}$)n | B. | an=4×($\frac{3}{2}$)n-1 | C. | an=4×($\frac{2}{3}$)n | D. | an=4×($\frac{2}{3}$)n-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com