
【题目】已知直线![]() :
:![]() 和二次函数
和二次函数![]() ,若直线
,若直线![]() 与二次函数
与二次函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点.
两点.
(1)求直线![]() 在
在![]() 轴上的截距
轴上的截距![]() ;
;
(2)若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 点的坐标;
点的坐标;
(3)当![]() 时,是否存在直线
时,是否存在直线![]() 与圆
与圆![]() :
:![]() 相切?若存在,求线段
相切?若存在,求线段![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:
【题目】2017年“双节”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速![]() 分成六段:
分成六段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.
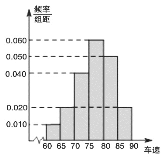
(1)调查公司在采样中,用到的是什么抽样方法?
(2)求这40辆小型车辆车速的众数、中位数及平均数的估计值;
(3)若从车速在![]() 的车辆中任抽取2辆,求车速在
的车辆中任抽取2辆,求车速在![]() 的车辆至少有一辆的概率.
的车辆至少有一辆的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到了一声巨响,正东观测点听到的时间比其它两观测点晚4![]() .已知各观测点到该中心的距离是1020
.已知各观测点到该中心的距离是1020![]() .则该巨响发生在接报中心的( )处.(假定当时声音传播的速度为340
.则该巨响发生在接报中心的( )处.(假定当时声音传播的速度为340![]() ,相关各点均在同一平面上)
,相关各点均在同一平面上)
A. 西偏北![]() 方向,距离
方向,距离![]() B. 东偏南
B. 东偏南![]() 方向,距离
方向,距离![]()
C. 西偏北![]() 方向,距离
方向,距离![]() D. 东偏南
D. 东偏南![]() 方向,距离
方向,距离![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一张坐标纸上一已作出圆![]() 及点
及点![]() ,折叠此纸片,使
,折叠此纸片,使![]() 与圆周上某点
与圆周上某点![]() 重合,每次折叠都会留下折痕,设折痕与直线
重合,每次折叠都会留下折痕,设折痕与直线![]() 的交点为
的交点为![]() ,令点
,令点![]() 的轨迹为
的轨迹为![]() .
.
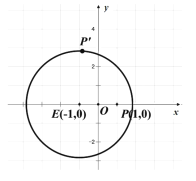
(1)求轨迹![]() 的方程;
的方程;
(2)若直线![]() 与轨迹
与轨迹![]() 交于两个不同的点
交于两个不同的点![]() ,且直线
,且直线![]() 与以
与以![]() 为直径的圆相切,若
为直径的圆相切,若![]() ,求
,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下五个关于圆锥曲线的命题中:
①平面内与定点A(-3,0)和B(3,0)的距离之差等于4的点的轨迹为![]() ;
;
②点P是抛物线![]() 上的动点,点P在y轴上的射影是M点A的坐标是A(3,6),则
上的动点,点P在y轴上的射影是M点A的坐标是A(3,6),则![]() 的最小值是6;
的最小值是6;
③平面内到两定点距离之比等于常数![]() 的点的轨迹是圆;
的点的轨迹是圆;
④若过点C(1,1)的直线![]() 交椭圆
交椭圆![]() 于不同的两点A,B,且C是AB的中点,则直线
于不同的两点A,B,且C是AB的中点,则直线![]() 的方程是
的方程是![]() .
.
⑤已知P为抛物线![]() 上一个动点,Q为圆
上一个动点,Q为圆![]() 上一个动点,那么点P到点Q的距离与点P到抛物线的准线距离之和的最小值是
上一个动点,那么点P到点Q的距离与点P到抛物线的准线距离之和的最小值是![]()
其中真命题的序号是______.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市的电视发射搭CD建在市郊的一座小山上,如图所示,小山高BC为30米,在地平面上有一点A,测得A,C两点间距离为50米.

(1)如果从点A观测电视发射塔的视角∠CAD=![]() ,求这座电视发射塔的高度;
,求这座电视发射塔的高度;
(2)点A在何位置时,角∠CAD最大.(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学参加语、数、外三门课程的考试,设该同学语、数、外取得优秀成绩的概率分别为![]() ,
, ![]() ,
, ![]() (
(![]() ),设该同学三门课程都取得优秀成绩的概率为
),设该同学三门课程都取得优秀成绩的概率为![]() ,都未取得优秀成绩的概率为
,都未取得优秀成绩的概率为![]() ,且不同课程是否取得优秀成绩相互独立.
,且不同课程是否取得优秀成绩相互独立.
(1)求![]() ,
, ![]() ;
;
(2)设![]() 为该同学取得优秀成绩的课程门数,求
为该同学取得优秀成绩的课程门数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点, ![]() 轴正半轴为极轴,取相同的长度单位建立极坐标系,曲线
轴正半轴为极轴,取相同的长度单位建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)在平面直角坐标系中,将曲线![]() 的纵坐标不变,横坐标变为原来的2倍,得到曲线
的纵坐标不变,横坐标变为原来的2倍,得到曲线![]() ,过点
,过点![]() 作直线
作直线![]() ,交曲线
,交曲线![]() 于
于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程与直线
的普通方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com