
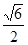 .
.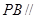 平面
平面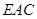 ,根据线面平行的判定定理,只需证明
,根据线面平行的判定定理,只需证明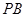 平行于平面
平行于平面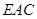 中的一条直线.连接
中的一条直线.连接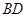 交
交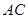 于
于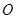 ,连接
,连接 ,因为
,因为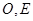 分别为
分别为 的中点,根据三角形的中位线的性质,可知
的中点,根据三角形的中位线的性质,可知 ,从而问题得证;
,从而问题得证;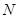 为
为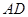 中点,连接
中点,连接 ,则
,则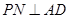 ,从而可得
,从而可得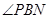 为直线
为直线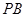 与平面
与平面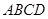 所成的角,进而可求
所成的角,进而可求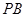 与平面
与平面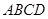 所成角正切值;
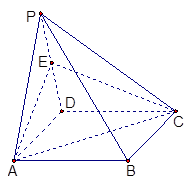
所成角正切值;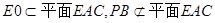 ,所以PB//平面EAC。 5分
,所以PB//平面EAC。 5分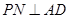 6分
6分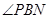 为直线PB与平面ABCD所成的角, 8分
为直线PB与平面ABCD所成的角, 8分
 又AD=2AB=2,则PN=
又AD=2AB=2,则PN=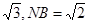 , 10分
, 10分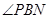 =
= , 12分;所以PB与平面ABCD所成角正切为值
, 12分;所以PB与平面ABCD所成角正切为值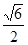 13分
13分

科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

| A.平面ABC⊥平面ABD |
| B.平面ABD⊥平面BDC |
| C.平面ABC⊥平面BDE,且平面ADC⊥平面BDE |
| D.平面ABC⊥平面ADC,且平面ADC⊥平面BDE |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
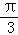 ,F为PC的中点,AF⊥PB.
,F为PC的中点,AF⊥PB.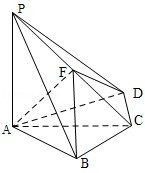
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com