
分析 (1)列举出所有满足“x∈A,y∈B,且均为整数”的基本事件的总个数,及其中满足条件x>y的基本事件的个数,代入古典概型概率计算公式,即可得到答案.
(2)画出满足x∈A,y∈B,且均为实数的基本事件对应的平面区域,及其中满足条件x>y的平面区域,代入几何概型概率计算公式,即可得到答案.
解答 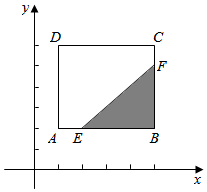 解:设事件A:”x>y”
解:设事件A:”x>y”
基本事件有:(1,2),(1,3),(1,4),(1,5),(1,6),(2,2),(2,3),(2,4),(2,5),(2,6),(3,2),(3,3),(3,4),(3,5),(3,6),(4,2),(4,3),(4,4),(4,5),(4,6),(5,2),(5,3)(5,4)(5,5)(5,6)共25个.( 3分)
(1)其中事件A包含的基本事件有(3,2),(4,2),(4,3),(5,2),(5,3),(5,4)共6个. ( 4分)
∴P(A)=$\frac{6}{25}$ ( 5分)
(2)设事件B:”x>y”(画图 (6分)
总基本事件{(x,y)|$\left\{\begin{array}{l}{1≤x≤5}\\{2≤y≤5}\end{array}\right.$},其对应的平面区域如图中矩形部分所示 7分
其中事件B:”x>y”{(x,y)|$\left\{\begin{array}{l}{1≤x≤5}\\{2≤y≤6}\\{x>y}\end{array}\right.$} 8分
所围成的面积为图中阴影部份.
E的坐标为(2,2),F的坐标为(5,5),B的坐标为(5,2)
P(B)=$\frac{{S}_{△BEF}}{{S}_{ABCD}}$=$\frac{\frac{9}{2}}{16}$=$\frac{9}{32}$ (10分)
点评 本题考查的知识点是列举法计算基本事件个数及事件发生的概率,古典概型及其概率计算公式,几何概型,其中古典概率由于基本事件有限可以用列举法表示,但几何概型的基本事件有无限多个,故求出其基本事件对应的几何图形的长度(面积/角度/体积)是解答的关键.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:高中数学 来源: 题型:选择题
 如图,已知两灯塔A,D相距20海里,甲、乙两船同时从灯塔A处出发,分别沿与AD所成角相等的两条航线AB,AC航行,经过一段时间分别到达B,C两处,此时恰好B,D,C三点共线,且∠ABD=$\frac{π}{3}$,∠ADC=$\frac{7π}{12}$,则乙船航行的距离AC为( )
如图,已知两灯塔A,D相距20海里,甲、乙两船同时从灯塔A处出发,分别沿与AD所成角相等的两条航线AB,AC航行,经过一段时间分别到达B,C两处,此时恰好B,D,C三点共线,且∠ABD=$\frac{π}{3}$,∠ADC=$\frac{7π}{12}$,则乙船航行的距离AC为( )| A. | 10$\sqrt{6}$+10$\sqrt{2}$海里 | B. | 10$\sqrt{6}$-10$\sqrt{2}$海里 | C. | 40海里 | D. | 10$\sqrt{6}$+10$\sqrt{3}$海里 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
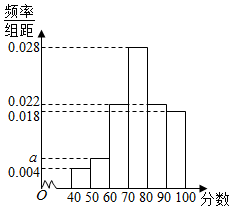 如图是根据某班50名同学在某次数学测验中的成绩(百分制)绘制的概率分布直方图,其中成绩分组区间为:[40,50),[50,60),…,[80,90),[90,100].
如图是根据某班50名同学在某次数学测验中的成绩(百分制)绘制的概率分布直方图,其中成绩分组区间为:[40,50),[50,60),…,[80,90),[90,100].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 随机抽取高一年级n名学生,测得他们的身高分别是a1,a2,…,an,则如图所示的程序框图输出的s=$\frac{{{a_1}-{a_2}+…+{{(-1)}^{n+1}}{a_n}}}{n}$.
随机抽取高一年级n名学生,测得他们的身高分别是a1,a2,…,an,则如图所示的程序框图输出的s=$\frac{{{a_1}-{a_2}+…+{{(-1)}^{n+1}}{a_n}}}{n}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,0) | B. | (1,0) | C. | (1,-3) | D. | (-1,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com