
分析 (1)a3=$\frac{41}{20}$=$\frac{1}{2}{a}_{2}$+$\frac{2}{{a}_{2}}$,解得a2=$\frac{5}{2}$或$\frac{8}{5}$,进而解得a1.
(2)对p,q分类讨论,对n分类讨论,利用等差数列与等比数列的前n项和公式即可得出.
(3)由题意,an>0,由a1=2,可得${a_2}=2p+\frac{1}{2}<2$,解得$0<p<\frac{3}{4}$,若数列{an}是单调递减数列,则${a_{n+1}}=p{a_n}+\frac{1}{a_n}<{a_n}$,可得${a_n}>\frac{1}{{\sqrt{1-p}}}$,可得:对于任意自然数n,$\frac{{\sqrt{1-p}}}{p}<{a_n}<{p^{n-1}}({2-\frac{1}{{\sqrt{1-p}}}})+\frac{1}{{\sqrt{1-p}}}$恒成立.由$0<p<\frac{3}{4}$,由$\frac{{\sqrt{1-p}}}{p}<\frac{1}{{\sqrt{1-p}}}$,解得$p>\frac{1}{2}$.下面证明:当$p∈({\frac{1}{2},\frac{3}{4}})$时,数列{an}是单调递减数列.通过作差即可证明.
解答 解:(1)∵a3=$\frac{41}{20}$=$\frac{1}{2}{a}_{2}$+$\frac{2}{{a}_{2}}$,解得a2=$\frac{5}{2}$或$\frac{8}{5}$,
当${a_2}=\frac{5}{2}$时,$\frac{5}{2}=\frac{1}{2}{a}_{1}+\frac{2}{{a}_{1}}$,解得a1=1或4,
当${a_2}=\frac{8}{5}$时,无解.
∴a1=1或4.
(2)若p=0,q≠0,${a_{n+1}}=\frac{q}{a_n}$.∴${a_1}=5,{a_2}=\frac{q}{5},{a_3}=5,{a_4}=\frac{q}{5}$,
∴当n为奇数时,${S_n}=5•\frac{n-1}{2}+\frac{q}{5}•\frac{n+1}{2}=\frac{25n+qn+q-25}{10}$;
当n为偶数时,${S_n}=5•\frac{n}{2}+\frac{q}{5}•\frac{n}{2}=\frac{25n+qn}{10}$.
若p≠0,q=0时,an+1=p•an,
∴${S_n}=\left\{{\begin{array}{l}{\frac{{5({p^n}-1)}}{p-1}}&{p≠0,p≠1}\\{5n}&{p=1}\end{array}}\right.$.
(3)由题意,an>0,
由a1=2,可得${a_2}=2p+\frac{1}{2}<2$,解得$0<p<\frac{3}{4}$,
若数列{an}是单调递减数列,则${a_{n+1}}=p{a_n}+\frac{1}{a_n}<{a_n}$,可得${a_n}>\frac{1}{{\sqrt{1-p}}}$,
又有${a_{n+1}}-\frac{1}{{\sqrt{1-p}}}=({{a_n}-\frac{1}{{\sqrt{1-p}}}})({p-\frac{{\sqrt{1-p}}}{a_n}})$①
∵${a_n}>\frac{1}{{\sqrt{1-p}}}$,∴$p-\frac{{\sqrt{1-p}}}{a_n}>0$,即${a_n}>\frac{{\sqrt{1-p}}}{p}$.
由①可知,${a_{n+1}}-\frac{1}{{\sqrt{1-p}}}<p•({{a_n}-\frac{1}{{\sqrt{1-p}}}})$,
∴${a_n}-\frac{1}{{\sqrt{1-p}}}<p•({{a_{n-1}}-\frac{1}{{\sqrt{1-p}}}})<…<{p^{n-1}}({{a_1}-\frac{1}{{\sqrt{1-p}}}})={p^{n-1}}({2-\frac{1}{{\sqrt{1-p}}}})$,
∴${a_n}<{p^{n-1}}({2-\frac{1}{{\sqrt{1-p}}}})+\frac{1}{{\sqrt{1-p}}}$②
∴对于任意自然数n,$\frac{{\sqrt{1-p}}}{p}<{a_n}<{p^{n-1}}({2-\frac{1}{{\sqrt{1-p}}}})+\frac{1}{{\sqrt{1-p}}}$恒成立.
∵$0<p<\frac{3}{4}$,由$\frac{{\sqrt{1-p}}}{p}<\frac{1}{{\sqrt{1-p}}}$,解得$p>\frac{1}{2}$.
下面证明:当$p∈({\frac{1}{2},\frac{3}{4}})$时,数列{an}是单调递减数列.
当$p<\frac{3}{4}$时,可得${a_2}=2p+\frac{1}{2}<2={a_1}$③
由${a_{n+1}}=p•{a_n}+\frac{1}{a_n}$和${a_n}=p•{a_{n-1}}+\frac{1}{{{a_{n-1}}}},(n≥2)$,
两式相减得${a_{n+1}}-{a_n}=({a_n}-{a_{n-1}})(p-\frac{1}{{{a_n}{a_{n-1}}}})$,
∵${a_n}=p•{a_{n-1}}+\frac{1}{{{a_{n-1}}}}≥2\sqrt{p}$成立,则有an•an-1>4p
当$p>\frac{1}{2}$时,${a_n}•{a_{n-1}}>4p>\frac{1}{p}$,即$p>\frac{1}{{{a_n}{a_{n-1}}}}$④,
由③④可知,当an<an-1时,恒有an+1<an,
对于任意的自然数n,an+1<an恒成立.
∴实数p的取值范围是:$(\frac{1}{2},\frac{3}{4})$.
点评 本题考查了递推关系、等差数列与等比数列的前n项和公式、不等式的解法与性质、数列的单调性,考查了分类讨论方法、推理能力与计算能力,属于难题.


 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
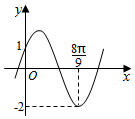
| A. | $\sqrt{3}$ | B. | 1 | C. | -1 | D. | -$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com