练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．若一个几何体的三视图如下图所示，则这个几何体是（　　）
    A．三棱锥B．四棱锥C．三棱柱D．四棱柱

    分析 由已知中的三视图，可得该几何体是一个四棱锥．

    解答 解：由正视图和侧视图均为三角形，
    可知该几何体是一个锥体，
    再由俯视图知底面为矩形，
    可得该几何体是一个四棱锥，
    故选：B

    点评 本题考查的知识点是简单几何体的三视图，难度不大，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    20．在直角坐标系xOy上取两个定点A1（-$\sqrt{6}$，0），A2（$\sqrt{6}$，0），再取两个动点N1（0，m），N2（0，n），且mn=2．
    （Ⅰ）求直线A1N1与A2N2交点M的轨迹C的方程；
    （Ⅱ）过R（3，0）的直线与轨迹C交于P，Q，过P作PN⊥x轴且与轨迹C交于另一点N，F为轨迹C的右焦点，若$\overrightarrow{RP}$=λ$\overrightarrow{RQ}$（λ＞1），求证：$\overrightarrow{NF}$=λ$\overrightarrow{FQ}$．

    查看答案和解析>>

    科目：高中数学 来源：2017届湖南衡阳县四中高三9月月考数学（文）试卷（解析版） 题型：选择题

    具有性质：的函数，我们称为满足“倒负”变换的函数，下列函数：

    ①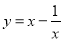；②；③其中满足“倒负”变换的函数是（ ）

    A．①② B．①③ C．②③ D．①

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．如图，在四棱椎P-ABCD中，侧棱PD⊥底面ABCD，底面ABCD为梯形，AB∥CD，∠BAD=∠ADC=90°，DC=2AB=2，DA=PD=$\sqrt{3}$，E为BC的中点，连结AE，交BD于点O．
    （Ⅰ）求证：AE⊥平面PBD；
    （Ⅱ）求二面角D-PB-E的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．求函数y=9-x2的导数（导函数）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知函数f（x）=x2ex+lnt-a，若对任意的t∈[1，e]，f（x）在区间[-1，1]总存在唯一的零点，则实数a的取值范围是（　　）
    A．[1，e]B．$（1+\frac{1}{e}，e]$C．（1，e]D．$[1+\frac{1}{e}，e]$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．将函数f（x）=$\sqrt{2}$sin2x-$\sqrt{2}$cos2x+1的图象向左平移$\frac{π}{4}$个单位，再向下平移1个单位，得到函数y=g（x）的图象，则下列关予函数y=g（x）的说法错误的是（　　）
    A．函数y=g（x）的最小正周期为π
    B．函数y=g（x）的图象的一条对称轴为直线x=$\frac{π}{8}$
    C．${∫}_{0}^{\frac{π}{2}}$g（x）dx=$\sqrt{2}$
    D．函数y=g（x）在区间[$\frac{π}{12}$，$\frac{5π}{8}$]上单调递减

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知g（x）=mx+2，f（x）=x2-2x，若对?x1∈[-1，2]．?x0∈[-1，2]，有g（x1）=f（x0）成立，则m的取值范围是[-1，$\frac{1}{2}$]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．下列函数中，与函数y=ln（x-1）定义域相同的是（　　）
    A．$y=\frac{1}{x-1}$B．$y={（x-1）^{-\frac{1}{2}}}$C．y=ex-1D．$y=\sqrt{sin（x-1）}$

    查看答案和解析>>

    同步练习册答案