
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 把定义域分成[$\frac{3}{2}$,2)和[2,3),利用分段函数表示出f(x)的解析式,求出f(x)的值域,根据值域的形式判断两段值域的端点大小,列出不等式解出n.
解答 解:当x∈[$\frac{3}{2}$,2)时,[x]=1,∴f(x)=${C}_{n}^{x}$=$\frac{n}{x}$,∴f(x)在[$\frac{3}{2}$,2)上是减函数,∴f(x)在[$\frac{3}{2}$,2)上的值域为($\frac{n}{2}$,$\frac{2n}{3}$].
当x∈[2,3)时,[x]=2,∴f(x)=${C}_{n}^{x}$=$\frac{n(n-1)}{x(x-1)}$,∴f(x)在[2,3)上是减函数,∴f(x)在[2,3)上的值域为($\frac{{n}^{2}-n}{6}$,$\frac{{n}^{2}-n}{2}$].
∵函数$f(x)=C_n^x$的值域是(a,b]∪(c,d],∴$\frac{2n}{3}$<$\frac{{n}^{2}-n}{6}$或$\frac{{n}^{2}-n}{2}$<$\frac{n}{2}$.解得n>5或0<n<2.
∵n>1,n∈N*,∴n的最小值是6.
故选:B.
点评 本题考查了分段函数的值域,新定义的理解,属于中档题.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,-4,6) | B. | (-6,-6,-5) | C. | (10,0,7) | D. | (10,-6,19) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
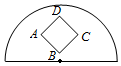 如图,在半径为1的半圆内,放置一个边长为$\frac{1}{2}$的正方形ABCD,向半圆内任取一点,则该点落在正方形内的槪率为( )
如图,在半径为1的半圆内,放置一个边长为$\frac{1}{2}$的正方形ABCD,向半圆内任取一点,则该点落在正方形内的槪率为( )| A. | $\frac{1}{π}$ | B. | $\frac{1}{2π}$ | C. | $\frac{2}{π}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com