
分析 (1)根据周期求出f(x)解析式,代入数值计算;
(2)根据θ的范围求出sinθ,使用诱导公式求出答案.
解答 解:(1)∵f(x)图象上相邻两个最高点的距离为2π,
∴f(x)的周期T=$\frac{2π}{ω}=2π$,∴ω=1.
∴f(x)=$\sqrt{2}cos$(x-$\frac{π}{12}$).
∴f(-$\frac{π}{6}$)=$\sqrt{2}$cos(-$\frac{π}{4}$)=1.
(2)∵θ∈($\frac{3π}{2}$,2π),∴sinθ=-$\sqrt{1-co{s}^{2}θ}$=-$\frac{4}{5}$.
∴f($θ+\frac{7π}{12}$)=$\sqrt{2}$cos(θ$+\frac{π}{2}$)=-$\sqrt{2}$sinθ=$\frac{4\sqrt{2}}{5}$.
点评 本题考查了余弦函数的图象与性质,同角三角函数的关系,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
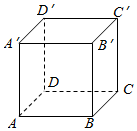 如图,正方体ABCD-A′B′C′D′的棱长为2,动点E,F在棱D′C′上.点G是AB的中点,动点P在棱A′A上,若EF=1,D′E=m,AP=n,则三棱锥P-EFG的体积( )
如图,正方体ABCD-A′B′C′D′的棱长为2,动点E,F在棱D′C′上.点G是AB的中点,动点P在棱A′A上,若EF=1,D′E=m,AP=n,则三棱锥P-EFG的体积( )| A. | 与m,n都有关 | B. | 与m,n都无关 | C. | 与m有关,与n无关 | D. | 与n有关,与m无关 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com