
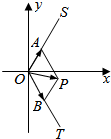
 如图所示,A(m,$\sqrt{3}$m)和B(n,-$\sqrt{3}$n)两点分别在射线OS,OT(点S,T分别在第一,四象限)上移动,且$\overrightarrow{OA}$•$\overrightarrow{OB}$=-$\frac{1}{2}$,O为坐标原点,动点P满足$\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$.
如图所示,A(m,$\sqrt{3}$m)和B(n,-$\sqrt{3}$n)两点分别在射线OS,OT(点S,T分别在第一,四象限)上移动,且$\overrightarrow{OA}$•$\overrightarrow{OB}$=-$\frac{1}{2}$,O为坐标原点,动点P满足$\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$.分析 (I)由向量数量积$\overrightarrow{OA}$•$\overrightarrow{OB}$=-$\frac{1}{2}$的坐标运算即可求得m•n的值;
(II)欲求P点的轨迹C的方程,设点P(x,y),只须求出其坐标x,y的关系式即可,由题意向量关系将x,y用m,n表示,最后消去m,n得到一个关系式,即得点P的轨迹方程.
解答 解:(Ⅰ)由题,$\overrightarrow{OA}•\overrightarrow{OB}=(m,\sqrt{3}m)•(n,-\sqrt{3}n)=-2mn=-\frac{1}{2}$.
所以$mn=\frac{1}{4}$.(4分)
(Ⅱ)设P(x,y)(x>0),由$\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{OB}$,得:$(x,y)=(m,\sqrt{3}m)+(n,-\sqrt{3}n)=(m+n,\sqrt{3}m-\sqrt{3}n)$,(6分)
令$\left\{\begin{array}{l}x=m+n\\ y=\sqrt{3}m-\sqrt{3}n\end{array}\right.$则${x^2}-\frac{y^2}{3}=4mn$,(8分)
又$mn=\frac{1}{4}$,所以,动点P的轨迹方程为${x^2}-\frac{y^2}{3}=1(x>0)$.(10分)
表示以原点为中心,焦点在x轴上,实轴长为2,焦距为4的双曲线${x^2}-\frac{y^2}{3}=1$右支.(12分)
点评 本小题主要考查曲线与方程,直线和圆锥曲线等基础知识,以及求直线方程的基本技能和综合运用数学知识解决问题的能力.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 3 | C. | 3$\sqrt{3}$ | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | 5 | C. | 8 | D. | -5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 | 5 |
| y | 5 | 9 | 10 | 11 | 15 |
| A. | 1.2 | B. | 2.2 | C. | 3.2 | D. | 4.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
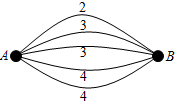 如图,A,B两点之间有5条网线并联,它们能通过的信息量分别为2、3、3、4、4.现从中随机任取2条网线.
如图,A,B两点之间有5条网线并联,它们能通过的信息量分别为2、3、3、4、4.现从中随机任取2条网线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com