
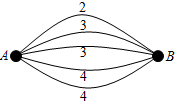
 如图,A,B两点之间有5条网线并联,它们能通过的信息量分别为2、3、3、4、4.现从中随机任取2条网线.
如图,A,B两点之间有5条网线并联,它们能通过的信息量分别为2、3、3、4、4.现从中随机任取2条网线.分析 (1)随机任取2条网线共有10种不同的情况,直接求解概率即可.
(2)求出选取的2条网线的概率,利用数学期望求解即可.
解答 (理科)解:(1)随机任取2条网线共有10种不同的情况.
∵2+4=3+3=6,
∴$P(x=6)=\frac{2+1}{10}=\frac{3}{10}$,…2'
∵3+4=7,∴$P(x=7)=\frac{4}{10}$,…4'
∵4+4=8,∴$P(x=8)=\frac{1}{10}$,…6'
∴$P(x≥6)=\frac{3}{10}+\frac{4}{10}+\frac{1}{10}=\frac{8}{10}=\frac{4}{5}$…8'
(2)∵$2+3=5,P(x=5)=\frac{2}{10}=\frac{1}{5}$,…10'
∴线路通过信息量的数学期望是$E(x)=5×\frac{1}{5}+6×\frac{3}{10}+7×\frac{4}{10}+8×\frac{1}{10}=6.4$…13'
答:(1)线路信息畅通的概率是$\frac{4}{5}$; (2)线路通过信息量的数学期望是6.4…14'
点评 本题考查离散型随机变量的期望的求法,考查计算能力.


科目:高中数学 来源: 题型:解答题
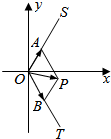 如图所示,A(m,$\sqrt{3}$m)和B(n,-$\sqrt{3}$n)两点分别在射线OS,OT(点S,T分别在第一,四象限)上移动,且$\overrightarrow{OA}$•$\overrightarrow{OB}$=-$\frac{1}{2}$,O为坐标原点,动点P满足$\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$.
如图所示,A(m,$\sqrt{3}$m)和B(n,-$\sqrt{3}$n)两点分别在射线OS,OT(点S,T分别在第一,四象限)上移动,且$\overrightarrow{OA}$•$\overrightarrow{OB}$=-$\frac{1}{2}$,O为坐标原点,动点P满足$\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10$\sqrt{6}$ | B. | 5$\sqrt{6}$ | C. | 30 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
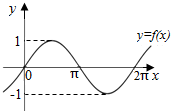
| A. | m | B. | 2m | C. | -m | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com