
| A. | a<b<c | B. | c>b>a | C. | c<a<b | D. | c>a>b |
分析 令g(x)=xf(x),根据当x∈(-∞,0)时,xf′(x)<f(-x),函数y=f(x)是定义在R上的奇函数,可得g′(x)=xf′(x)+f(x)<0,即函数g(x)在(-∞,0)时单调递减,在函数g(x)在(0,+∞)单调递增,问题得以解决.
解答 解:令g(x)=xf(x),
∵当x∈(-∞,0)时,xf′(x)<f(-x),函数y=f(x)是定义在R上的奇函数,
∴可以化为xf′(x)+f(x)<0,
∴g′(x)=xf′(x)+f(x)<0,
∴函数g(x)在(-∞,0)单调递减,
∵g(-x)=-xf(-x)=xf(x)=g(x),
∴g(x)为偶函数,
∴函数g(x)在(0,+∞)单调递增,
∴g(log2$\frac{1}{4}$)=g(-2)=g(2)
∵2>$\sqrt{3}$>lg3,
∴c>a>b.
故选:D.
点评 本题考查了利用导数研究函数的单调性、对数函数的单调性,考查了推理能力与计算能力,属于中档题


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
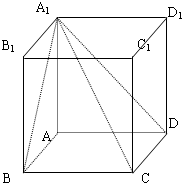 如图,长方体ABCD-A1B1C1D1的AA1=1,底面ABCD的周长为4.
如图,长方体ABCD-A1B1C1D1的AA1=1,底面ABCD的周长为4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | [-8,-1] | B. | [-10,0] | C. | [-10,6] | D. | (-6,6] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若a-b=1,则a2+b2>$\frac{1}{2}$”是真命题 | |
| B. | “a=b=$\frac{1}{2}$”是“$\frac{1}{a}+\frac{1}{b}$=4”的必要不充分条件 | |
| C. | 若非空集合A,B,C满足A∪B=C,且B不是A的子集,则“x∈C”是“x∈A”的充分不必要条件 | |
| D. | 命题“?x0∈R,x02+1≤2x0”的否定是“?x∈R,x2+1>2x” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 029,051 | B. | 036,052 | C. | 037,053 | D. | 045,054 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com