
���� ���� ���������ݼ�������ֱ������Ļ�����ʽ�������C1��ֱ�����귽�̣�������C2�IJ��������еIJ�����ȥ��ת��Ϊ��ͨ���̣�
��������C1��C2����������������б�ʽ������ɵ�����C1��C2���ཻ�������㣻���������Ľ⣬�ɵ�������������꣬�Ӷ�����������ľ��룮
��� �⣺����������C1�ļ����귽��Ϊ�ѣ�sin��+cos�ȣ�=1���ɵ�����ֱ�����귽��Ϊx+y=1��
��������C2�IJ�������Ϊ$\left\{\begin{array}{l}{x=2cos��}\\{y=sin��}\end{array}\right.$����Ϊ���������ɵ�������ͨ����Ϊ $\frac{{x}^{2}}{4}$+y2=1��
��������C1��C2������������ $\left\{\begin{array}{l}{x+y=1}\\{\frac{{x}^{2}}{4}{+y}^{2}=1}\end{array}\right.$������ɵ� 5x2-8x=0����Ȼ��=64��0��
������C1��C2���ཻ�������㣮
�ⷽ�������$\left\{\begin{array}{l}{x=0}\\{y=1}\end{array}\right.$���� $\left\{\begin{array}{l}{x=\frac{8}{5}}\\{y=-\frac{3}{5}}\end{array}\right.$���ɵ���2�����������ֱ�Ϊ��0��1������$\frac{8}{5}$��-$\frac{3}{5}$����
���� ������Ҫ����Ѽ����귽�̻�Ϊֱ�����귽�̣��Ѳ������̻�Ϊ��ͨ���̵ķ��������������ߵĽ��㣬���ڻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b��c | B�� | c��b��a | C�� | c��a��b | D�� | c��a��b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 1 | C�� | $\sqrt{2}$ | D�� | $2\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����������ABCD-A1B1C1D1�У�AB=BC=CA=$\sqrt{3}$��AD=CD=AA1=1��ƽ��AA1C1C��ƽ��ABCD��EΪ�߶�BC���е㣬
��ͼ����������ABCD-A1B1C1D1�У�AB=BC=CA=$\sqrt{3}$��AD=CD=AA1=1��ƽ��AA1C1C��ƽ��ABCD��EΪ�߶�BC���е㣬�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
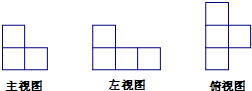
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-1��+�ޣ� | B�� | ��-�ޣ�-1]��[3��+�ޣ� | C�� | [-1��3] | D�� | ��-�ޣ�3] |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com