Question

5．如图，在△ABC中，AB=AC=1，∠BAC=120°，点P在以A为圆心，AB为半径的圆弧$\widehat{BC}$上运动．
（Ⅰ）若$\overrightarrow{PC}$•$\overrightarrow{PB}$取最小值，求∠BAP的大小；
（Ⅱ）设$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$，其中x，y∈R，求xy的最大值．

Answer 1

分析 （Ⅰ）设角BAP=α（0°≤α≤120°），则CAP=120°-α，利用向量的加法法则把$\overrightarrow{PC}$、$\overrightarrow{PB}$用$\overrightarrow{PA}、\overrightarrow{AB}、\overrightarrow{AC}$表示，代入$\overrightarrow{PC}$•$\overrightarrow{PB}$，进一步代入数量积转化为关于α的三角函数求解；
（Ⅱ）以AB所在直线为x轴，以A为坐标原点建立平面直角坐标系，得$\overrightarrow{AB}=（1，0）$，$\overrightarrow{AC}=（-\frac{1}{2}，\frac{\sqrt{3}}{2}）$，由$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$=（x-$\frac{1}{2}y$，$\frac{\sqrt{3}}{2}y$），结合$|\overrightarrow{PA}|=1$利用基本不等式求最值得到xy的最大值．

解答 解：（Ⅰ）设角BAP=α（0°≤α≤120°），则CAP=120°-α，由题意可知，$\overrightarrow{PB}=\overrightarrow{PA}+\overrightarrow{AB}$，$\overrightarrow{PC}=\overrightarrow{PA}+\overrightarrow{AC}$，
∴$\overrightarrow{PC}$•$\overrightarrow{PB}$=$（\overrightarrow{PA}+\overrightarrow{AC}）•（\overrightarrow{PA}+\overrightarrow{AB}）$=${\overrightarrow{PA}}^{2}+\overrightarrow{PA}•\overrightarrow{AB}+\overrightarrow{PA}•\overrightarrow{AC}+\overrightarrow{AC}•\overrightarrow{AB}$
=1+1×1×cos（180°-α）+1×1×cos（60°+α）+1×1×cos120°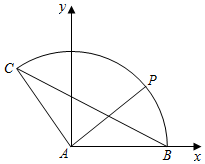
=1-cosα+cos60°cosα-sin60°sinα$-\frac{1}{2}$
=$-\frac{\sqrt{3}}{2}sinα-\frac{1}{2}cosα+\frac{1}{2}$=-sin（α+30°）$+\frac{1}{2}$．
∵0°≤α≤120°，
∴30°≤α+30°≤150°，
则当α+30°=90°，即α=60°时，$\overrightarrow{PC}$•$\overrightarrow{PB}$取最小值$-\frac{1}{2}$；
（Ⅱ）如图，以AB所在直线为x轴，以A为坐标原点建立平面直角坐标系，
则$\overrightarrow{AB}=（1，0）$，$\overrightarrow{AC}=（-\frac{1}{2}，\frac{\sqrt{3}}{2}）$，
则$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$=x（1，0）+y（$-\frac{1}{2}，\frac{\sqrt{3}}{2}$）=（x-$\frac{1}{2}y$，$\frac{\sqrt{3}}{2}y$），
∴$|\overrightarrow{AP}{|}^{2}=（x-\frac{y}{2}）^{2}+（\frac{\sqrt{3}y}{2}）^{2}$=${x}^{2}-xy+\frac{{y}^{2}}{4}+\frac{3{y}^{2}}{4}={x}^{2}+{y}^{2}-xy$=1，
∴1=x²+y²-xy≥2xy-xy=xy，
当且仅当x=y=1时，xy有最大值为1．

点评 本题考查平面向量的数量积运算，考查了向量模的求法，训练了利用基本不等式求最值，是中档题．