
分析 (1)证明数量积为零即可;
(2)使用向量的夹角公式计算cos∠ABC,得出sin∠ABC;
(3)使用勾股定理和定比分点性质求出.
解答 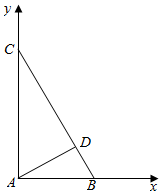 解:(1)$\overrightarrow{AB}=(2\sqrt{3},0)$,$\overrightarrow{AC}=(0,2\sqrt{6})$.
解:(1)$\overrightarrow{AB}=(2\sqrt{3},0)$,$\overrightarrow{AC}=(0,2\sqrt{6})$.
∴$\overrightarrow{AB}•\overrightarrow{AC}$=2$\sqrt{3}×0$$+0×2\sqrt{6}$=0,
∴$\overrightarrow{AB}⊥\overrightarrow{AC}$,即AB⊥AC.
(2)$\overrightarrow{BA}=(-2\sqrt{3},0)$,$\overrightarrow{BC}=(-2\sqrt{3},2\sqrt{6})$,
|$\overrightarrow{BA}$|=2$\sqrt{3}$,|$\overrightarrow{BC}$|=6,$\overrightarrow{BA}•\overrightarrow{BC}$=12.
∴cos∠ABC=$\frac{\overrightarrow{BA}•\overrightarrow{BC}}{|\overrightarrow{BA}||\overrightarrow{BC}|}$=$\frac{\sqrt{3}}{3}$.
∴sin∠ABC=$\sqrt{1-co{s}^{2}∠ABC}$=$\frac{\sqrt{6}}{3}$.
(3)∵AC=2$\sqrt{6}$,AB=2$\sqrt{3}$,BC=6,AB⊥AC,AD⊥BC,
∴AD=$\frac{AC×AB}{BC}=2\sqrt{2}$.
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=4.
∴D为BC上靠近B的三等分点.
∴D($\frac{4\sqrt{3}}{3}$,$\frac{2\sqrt{6}}{3}$).
点评 本题考查了向量在几何中的应用,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
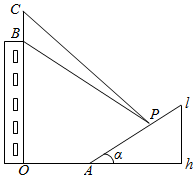 如图,某人在一小斜坡上的点P(坡高h=10m)观看对面一座大楼顶上的广告画,画高BC=8m,画所在的大楼高OB=22m,OA=20m,图上所示的山坡坡面可视为直线l,且点P在直线l上,l与水平地面的夹角为α,tanα=$\frac{1}{2}$.试问:此人所在的点P距水平地面多高时,观看广告画的视角∠BPC最大?(不计此人身高,楼OB与斜坡l在同一平面内)
如图,某人在一小斜坡上的点P(坡高h=10m)观看对面一座大楼顶上的广告画,画高BC=8m,画所在的大楼高OB=22m,OA=20m,图上所示的山坡坡面可视为直线l,且点P在直线l上,l与水平地面的夹角为α,tanα=$\frac{1}{2}$.试问:此人所在的点P距水平地面多高时,观看广告画的视角∠BPC最大?(不计此人身高,楼OB与斜坡l在同一平面内)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | BD=2CD | B. | BD=CD | C. | BD=3CD | D. | CD=2BD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com