
分析 先求出cosA=±$\sqrt{1-si{n}^{2}A}$=±$\frac{3}{5}$,再由cosB=$\sqrt{\frac{1-cosA}{2}}$,能求出cosB.
解答 解:∵等腰三角形ABC中,AB=AC,且sinA=$\frac{4}{5}$,
∴cosA=±$\sqrt{1-si{n}^{2}A}$=±$\sqrt{1-\frac{16}{25}}$=±$\frac{3}{5}$,
当cosA=$\frac{3}{5}$时,cosA=cos(π-2B)=-cos2B=1-2cos2B,
∴cosB=$\sqrt{\frac{1-cosA}{2}}$=$\frac{\sqrt{5}}{5}$,
当cosA=-$\frac{3}{5}$时,cosA=cos(π-2B)=-cos2B=1-2cos2B,
∴cosB=$\sqrt{\frac{1-cosA}{2}}$=$\frac{2\sqrt{5}}{5}$.
故答案为:$\frac{\sqrt{5}}{5}$或$\frac{2\sqrt{5}}{5}$.
点评 本题考查三角函数值的求法,是中档题,解题时要认真审题,注意同角三角函数关系式、二倍角公式的合理运用.


科目:高中数学 来源: 题型:选择题
| 价格x | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y | 11 | 10 | 8 | 6 | 5 |
| A. | 24 | B. | 35.6 | C. | 40 | D. | 40.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{7}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{7}}{7}$或$\frac{5}{7}$ | D. | $\frac{5}{7}$或$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
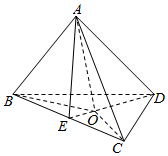 在平面几何里,有勾股定理:“设△ABC的两边AB、AC互相垂直,则AB2+AC2=BC2”.拓展到空间(如图),类比平面几何的勾股定理,研究三棱锥的侧面面积与底面面积间的关系,可以得出的结论是设三棱锥A-BCD的三侧面ABC,ACD,ADB两两垂直,则S△BCD2 =S△ABC2+S△ACD2+S△ADB2.
在平面几何里,有勾股定理:“设△ABC的两边AB、AC互相垂直,则AB2+AC2=BC2”.拓展到空间(如图),类比平面几何的勾股定理,研究三棱锥的侧面面积与底面面积间的关系,可以得出的结论是设三棱锥A-BCD的三侧面ABC,ACD,ADB两两垂直,则S△BCD2 =S△ABC2+S△ACD2+S△ADB2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某公司领导层为了了解本公司的管理状况,从公司员工中随机抽取了25人,让他们对公司的管理水平打分(满分为100分)得到如下数据:69,82,81,76,84,79,77,77,65,84,69,83,71,76,89,74,73,83,78,82,72,74,86,79,76.
某公司领导层为了了解本公司的管理状况,从公司员工中随机抽取了25人,让他们对公司的管理水平打分(满分为100分)得到如下数据:69,82,81,76,84,79,77,77,65,84,69,83,71,76,89,74,73,83,78,82,72,74,86,79,76.| 分组 | 频数 | 频率 |
| [65,70) | ||
| [70,75) | ||
| [75,80) | ||
| [80,85) | ||
| [85,90[ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 钝角三角形 | B. | 直角三角形 | C. | 锐角三角形 | D. | 等边三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
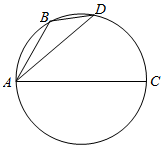 如图,B、D是以AC为直径的圆上的两点,其中AB=$\sqrt{t+1}$,AD=$\sqrt{t+2}$,则$\overrightarrow{AC}$•$\overrightarrow{BD}$=( )
如图,B、D是以AC为直径的圆上的两点,其中AB=$\sqrt{t+1}$,AD=$\sqrt{t+2}$,则$\overrightarrow{AC}$•$\overrightarrow{BD}$=( )| A. | 1 | B. | 2 | C. | t | D. | 2t |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com