练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．已知：在△ABC中，acosB=bcosA，则此三角形的形状为（　　）
    A．等腰三角形B．直角三角形
    C．等腰或直角三角形D．等腰直角三角形

    分析 根据正弦定理化简acosB=bcosA，利用两角差的正弦公式化简，根据三角形内角的范围判断出△ABC的形状．

    解答 解：由题意知，在△ABC中，acosB=bcosA，
    ∴根据正弦定理得：sinAcosB=sinBcosA，
    ∴sinAcosB-sinBcosA=0，则sin（A-B）=0，
    ∵A、B∈（0，π），∴-π＜A-B＜π，
    ∴A-B=0，则A=B，
    ∴△ABC是等腰三角形，
    故选：A．

    点评 本题考查正弦定理，以及两角差的正弦公式的应用，注意内角的范围，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

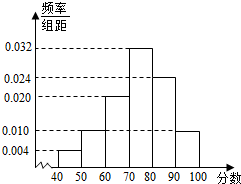    6．某校从高一年级学生中随机抽取50名学生，将他们的期中考试数学成绩（满分100分，成绩均为不低于40分的整数）分成六段：[40，50），[50，60），…，[90，100]，得到如图所示的频率分布直方图．
    （1）若该校高一年级共有学生1000人，试估计成绩不低于60分的人数；
    （2）为了帮助学生提高数学成绩，学校决定在随机抽取的50名学生中成立“二帮一”小组，即从成绩[90，100]中选两位同学，共同帮助[40，50）中的某一位同学．已知甲同学的成绩为42分，乙同学的成绩为95分，求甲、乙恰好被安排在同一小组的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．下列有关命题说法正确的是（　　）
    A．命题“若x2=4，则x=2”的否命题为“若x2=4，则x≠2”
    B．所有常数列既是等差数列也是等比数列
    C．命题“若x=y，则sinx=siny”的逆否命题为假命题
    D．命题“?x∈R，x2+x＜0”的否定是“?x∈R，x2+x≥0”．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知点P（-3，4）在角α的终边上，则$\frac{sinα+cosα}{3sinα+2cosα}$的值为（　　）
    A．-$\frac{1}{6}$B．$\frac{1}{6}$C．$\frac{7}{18}$D．-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．设f（x）=x2+bx+c，且f（-1）=f（3），则（　　）
    A．f（1）＞c＞f（-1）B．f（1）＜c＜f（-1）C．f（1）＞f（-1）＞cD．f（1）＜f（-1）＜c

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．若函数f（x）的定义域为[0，3]，则f（x2-1）的定义域为（　　）
    A．[0，9]B．[0，8]C．[-2，-1]∪[1，2]D．[1，2]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．（1）计算$\frac{{{{（1+i）}^2}}}{1+2i}+\frac{{{{（1-i）}^2}}}{2-i}$；
    （2）若实数x，y满足$\frac{x}{1+i}+\frac{y}{1+2i}=\frac{10}{1+3i}$，求x，y的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．设$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$是任意非零的平面向量，且互不共线，给出下面的五个命题：
    （1）|$\overrightarrow{a}$•$\overrightarrow{b}$|=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|；        （2）（$\overrightarrow{b}$•$\overrightarrow{c}$）$\overrightarrow{a}$-（$\overrightarrow{c}$•$\overrightarrow{a}$）$\overrightarrow{b}$不与向量$\overrightarrow{c}$垂直．；
    （3）|$\overrightarrow{a}$|-|$\overrightarrow{b}$|＜|$\overrightarrow{a}$-$\overrightarrow{b}$|；      （4）若$\overrightarrow{a}$•$\overrightarrow{b}$=0，则$\overrightarrow{a}$=0，或者$\overrightarrow{b}$=0；
    （5）（$\overrightarrow{a}$•$\overrightarrow{b}$）$\overrightarrow{c}$=（$\overrightarrow{b}$•$\overrightarrow{c}$）$\overrightarrow{a}$；     （6）（3$\overrightarrow{a}$+2$\overrightarrow{b}$）•（3$\overrightarrow{a}$-2$\overrightarrow{b}$）=9|$\overrightarrow{a}$|2-4|$\overrightarrow{b}$|2
    其中真命题的序号为（3）（6）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．设函数f（x）=$\sqrt{3}$cos2ωx+sinωxcosωx+a（其中ω＞0，a∈R），且f（x）的图象在y柱右侧的第一个最高点的横坐标为$\frac{π}{6}$．
    （1）求ω的值；
    （2）如果f（x）在区间[0，$\frac{π}{2}$]上有两个实数解，求a的取值范围．

    查看答案和解析>>

    同步练习册答案