
分析 (1)利用基本不等式的性质即可证明.
(2)利用上述结论即可得出.
解答 (1)证明:$(\frac{a^2}{x}+\frac{b^2}{y})m=(\frac{a^2}{x}+\frac{b^2}{y})(x+y)={a^2}+\frac{{{a^2}y}}{x}+\frac{{{b^2}x}}{y}+{b^2}≥{a^2}+2\sqrt{\frac{{{a^2}y}}{x}•\frac{{{b^2}x}}{y}}+{b^2}$
=a2+2ab+b2=(a+b)2,$\frac{a^2}{x}+\frac{b^2}{y}≥\frac{{(a+b{)^2}}}{m}$.
当且仅当$\frac{{{a^2}y}}{x}=\frac{{{b^2}x}}{y}$,即$\frac{a}{b}=\frac{x}{y}$时,等号成立.
(2)解:∵$x∈(0,\frac{1}{3})$,∴1-3x>0,
∴$f(x)=\frac{12}{x}+\frac{9}{1-3x}=(\frac{36}{3x}+\frac{9}{1-3x})•1=(\frac{6^2}{3x}+\frac{3^2}{1-3x})•[3x+(1-3x)]≥{(6+3)^2}=81$,
当且仅当$\frac{6}{3}=\frac{3x}{1-3x}$,即$x=\frac{2}{9}$时,f(x)min=81.
点评 本题考查了基本不等式的性质及其应用、函数的最值,考查了推理能力与计算能力,属于中档题.


 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
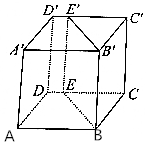 如图,过正方体ABCD-A′B′C′D′的棱BB′作一平面交平面CDD′C′于EE′,则BB′与EE′的位置关系是( )
如图,过正方体ABCD-A′B′C′D′的棱BB′作一平面交平面CDD′C′于EE′,则BB′与EE′的位置关系是( )| A. | 平行 | B. | 相交 | C. | 异面 | D. | 不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com