
分析 解法一:(Ⅰ)设点M(x,y),利用已知条件真假求解曲线C的方程.
(Ⅱ)求出E,F坐标,设P(-1,y0),S(x1,y1),T(x2,y2),写出直线PE的方程为y=y0(x+2),与轨迹方程联立,求出S、T坐标,通过kAS=kAT,说明A,S,T三点共线.
解法二:(Ⅰ)同解法一.
(Ⅱ)不妨设E(-2,0),F(2,0).设P(-1,y0),S(x1,y1),T(x2,y2),直线PE的方程为y=y0x+2y0,与轨迹方程联立,求出S、T坐标,通过kAS=kAT,说明A,S,T三点共线.
解法三:(Ⅰ)同解法一.
(Ⅱ)由(Ⅰ)知曲线C的方程为x2+y2=4,不妨设E(-2,0),F(2,0).设P(-1,y0),S(x1,y1),T(x2,y2),当y0=0时,S(-2,0),T(2,0),此时A,S,T三点共线.当y0≠0时,则直线PE的方程为y=y0x+2y0,与轨迹方程联立,求出S、T坐标,通过kAS-kAT=0,说明A,S,T三点共线.
解答 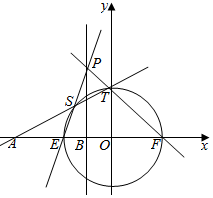 解法一:(Ⅰ)设点M(x,y),依题意,$\frac{{|{MA}|}}{{|{MB}|}}=\frac{{\sqrt{{{({x+4})}^2}+{y^2}}}}{{\sqrt{{{({x+1})}^2}+{y^2}}}}=2$,(3分)
解法一:(Ⅰ)设点M(x,y),依题意,$\frac{{|{MA}|}}{{|{MB}|}}=\frac{{\sqrt{{{({x+4})}^2}+{y^2}}}}{{\sqrt{{{({x+1})}^2}+{y^2}}}}=2$,(3分)
化简得x2+y2=4,即曲线C的方程为x2+y2=4.(5分)
(Ⅱ)由(Ⅰ)知曲线C的方程为x2+y2=4,
令y=0得x=±2,不妨设E(-2,0),F(2,0).
设P(-1,y0),S(x1,y1),T(x2,y2),
则直线PE的方程为y=y0(x+2),
由$\left\{\begin{array}{l}y={y_0}({x+2})\\{x^2}+{y^2}=4\end{array}\right.$得$({y_0^2+1}){x^2}+4y_0^2x+4y_0^2-4=0$,(6分)
所以$-2{x_1}=\frac{4y_0^2-4}{y_0^2+1}$,即${x_1}=\frac{2-2y_0^2}{y_0^2+1}$,${y_1}=\frac{{4{y_0}}}{y_0^2+1}$.(8分)
直线PF的方程为$y=-\frac{y_0}{3}({x-2})$,
由$\left\{\begin{array}{l}y=-\frac{y_0}{3}({x-2})\\{x^2}+{y^2}=4\end{array}\right.$得$({y_0^2+9}){x^2}-4y_0^2x+4y_0^2-36=0$,(9分)
所以$2{x_2}=\frac{4y_0^2-36}{y_0^2+9}$,即${x_2}=\frac{2y_0^2-18}{y_0^2+9}$,${y_2}=\frac{{12{y_0}}}{y_0^2+9}$.(11分)
所以${k_{AS}}=\frac{y_1}{{{x_1}+4}}=\frac{{\frac{{4{y_0}}}{y_0^2+1}}}{{\frac{2-2y_0^2}{y_0^2+1}+4}}=\frac{{2{y_0}}}{y_0^2+3}$,
${k_{AT}}=\frac{y_2}{{{x_2}+4}}=\frac{{\frac{{12{y_0}}}{y_0^2+9}}}{{\frac{2y_0^2-18}{y_0^2+9}+4}}=\frac{{2{y_0}}}{y_0^2+3}$,
所以kAS=kAT,所以A,S,T三点共线.(12分)
解法二:(Ⅰ)同解法一.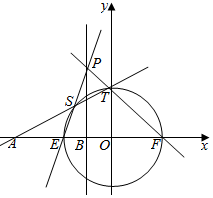
(Ⅱ)由(Ⅰ)知曲线C的方程为x2+y2=4,
令y=0得x=±2,不妨设E(-2,0),F(2,0).
设P(-1,y0),S(x1,y1),T(x2,y2),
则直线PE的方程为y=y0x+2y0,
由$\left\{\begin{array}{l}y={y_0}x+2{y_0}\\{x^2}+{y^2}=4\end{array}\right.$消去x得$({y_0^2+1}){y^2}-4{y_0}y=0$,(6分)
所以${y_1}=\frac{{4{y_0}}}{y_0^2+1}$,${x_1}=\frac{2-2y_0^2}{y_0^2+1}$.(8分)
直线PF的方程为$y=-\frac{y_0}{3}x+\frac{2}{3}{y_0}$,
由$\left\{\begin{array}{l}y=-\frac{y_0}{3}x+\frac{2}{3}{y_0}\\{x^2}+{y^2}=4\end{array}\right.$得$({y_0^2+9}){y^2}-12{y_0}y=0$,(9分)
所以${y_2}=\frac{{12{y_0}}}{y_0^2+9}$,${x_2}=\frac{2y_0^2-18}{y_0^2+9}$.(11分)
以下同解法一.
解法三:(Ⅰ)同解法一. (Ⅱ)由(Ⅰ)知曲线C的方程为x2+y2=4,
(Ⅱ)由(Ⅰ)知曲线C的方程为x2+y2=4,
令y=0得x=±2,不妨设E(-2,0),F(2,0).
设P(-1,y0),S(x1,y1),T(x2,y2),
当y0=0时,S(-2,0),T(2,0),此时A,S,T三点共线.
当y0≠0时,则直线PE的方程为y=y0x+2y0,
由$\left\{\begin{array}{l}y={y_0}x+2{y_0}\\{x^2}+{y^2}=4\end{array}\right.$消去x得$({y_0^2+1}){y^2}-4{y_0}y=0$,(6分)
所以${y_1}=\frac{{4{y_0}}}{y_0^2+1}$.(7分)
直线PF的方程为$y=-\frac{y_0}{3}x+\frac{2}{3}{y_0}$,
由$\left\{\begin{array}{l}y=-\frac{y_0}{3}x+\frac{2}{3}{y_0}\\{x^2}+{y^2}=4\end{array}\right.$消去x得$({y_0^2+9}){y^2}-12{y_0}y=0$,(8分)
所以${y_2}=\frac{{12{y_0}}}{y_0^2+9}$.(9分)
${k_{AS}}-{k_{AT}}=\frac{y_1}{{{x_1}+4}}-\frac{y_2}{{{x_2}+4}}$=$\frac{{{y_1}({{x_2}+4})-{y_2}({{x_1}+4})}}{{({{x_1}+4})({{x_2}+4})}}$=$\frac{{{y_1}({-\frac{{3{y_2}}}{y_0}+6})-{y_2}({\frac{y_1}{y_0}+2})}}{{({{x_1}+4})({{x_2}+4})}}$
=$\frac{{{y_1}({-3{y_2}+6{y_0}})-{y_2}({{y_1}+2{y_0}})}}{{{y_0}({{x_1}+4})({{x_2}+4})}}=\frac{{-4{y_1}{y_2}+6{y_0}{y_1}-2{y_0}{y_2}}}{{{y_0}({{x_1}+4})({{x_2}+4})}}$,(11分)
因为$6{y_0}{y_1}-2{y_0}{y_2}=\frac{24y_0^2}{y_0^2+1}-\frac{24y_0^2}{y_0^2+9}=\frac{192y_0^2}{{({y_0^2+1})({y_0^2+9})}}$,
$-4{y_1}{y_2}=-4×\frac{{4{y_0}}}{y_0^2+1}×\frac{{12{y_0}}}{y_0^2+9}=-\frac{192y_0^2}{{({y_0^2+1})({y_0^2+9})}}$,
所以-4y1y2+6y0y1-2y0y2=0.
所以kAS=kAT,所以A,S,T三点共线.(12分)
点评 本小题考查圆的方程、直线与圆的位置关系等基础知识,考查运算求解能力、推理论证能力,考查数形结合思想、化归与转化思想等.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{2}$,+∞) | B. | (1,$\sqrt{2}$) | C. | [$\sqrt{3}$,+∞) | D. | (1,$\sqrt{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\frac{1}{4}$x | B. | y=±$\frac{1}{3}$x | C. | y=±$\frac{1}{2}$x | D. | y=±2x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com