Question

12．根据教材P₄₅第6题可以证明函数g（x）=x²+ax+b满足性质$g（\frac{{{x_1}+{x_2}}}{2}）≤\frac{{g（{x_1}）+g（{x_2}）}}{2}$，理解其中的含义．对于函数f（x）=2^x，h（x）=log₂x及任意实数x₁，x₂，仿照上述理解，可以推测（　　）

• A． $f（\frac{{{x_1}+{x_2}}}{2}）≤\frac{{f（{x_1}）+f（{x_2}）}}{2}，h（\frac{{{x_1}+{x_2}}}{2}）≤\frac{{h（{x_1}）+h（{x_2}）}}{2}$
• B． $f（\frac{{{x_1}+{x_2}}}{2}）≥\frac{{f（{x_1}）+f（{x_2}）}}{2}，h（\frac{{{x_1}+{x_2}}}{2}）≥\frac{{h（{x_1}）+h（{x_2}）}}{2}$
• C． $f（\frac{{{x_1}+{x_2}}}{2}）≤\frac{{f（{x_1}）+f（{x_2}）}}{2}，h（\frac{{{x_1}+{x_2}}}{2}）≥\frac{{h（{x_1}）+h（{x_2}）}}{2}$
• D． $f（\frac{{{x_1}+{x_2}}}{2}）≥\frac{{f（{x_1}）+f（{x_2}）}}{2}，h（\frac{{{x_1}+{x_2}}}{2}）≤\frac{{h（{x_1}）+h（{x_2}）}}{2}$

Answer 1

分析 根据题意，由$g（\frac{{{x_1}+{x_2}}}{2}）≤\frac{{g（{x_1}）+g（{x_2}）}}{2}$，结合二次函数的性质分析其函数的图象中，任意2点的连线必须在图象的上方，进而由函数f（x）=2^x，h（x）=log₂x的图象性质分析可得答案．

解答 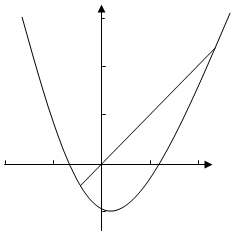解：根据题意，g（x）=x²+ax+b满足性质$g（\frac{{{x_1}+{x_2}}}{2}）≤\frac{{g（{x_1}）+g（{x_2}）}}{2}$，其函数的图象中，任意2点的连线必须在图象的上方，
如图：
反之若其图象中任意2点的连线必须在图象的下方，必有$g（\frac{{{x_1}+{x_2}}}{2}）≥\frac{{g（{x_1}）+g（{x_2}）}}{2}$，
对于函数f（x）=2^x，其图象中任意2点的连线必须在图象的上方，则必有$f（\frac{{{x_1}+{x_2}}}{2}）≤\frac{{f（{x_1}）+f（{x_2}）}}{2}$，
对于函数h（x）=log₂x，其图象中任意2点的连线必须在图象的下方，则必有$h（\frac{{{x_1}+{x_2}}}{2}）≥\frac{{h（{x_1}）+h（{x_2}）}}{2}$，
故选：C．

点评 本题考查函数的图象，关键在于分析题目中$g（\frac{{{x_1}+{x_2}}}{2}）≤\frac{{g（{x_1}）+g（{x_2}）}}{2}$，得到其对应函数图象应具有的性质．