练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．如图，直线l：y=x+b与抛物线C：x2=4y相切于点A．
    （1）求实数b的值；
    （2）求以点A为圆心，且与抛物线C的准线相切的圆的方程．

    分析 （1）由题意，联立方程组，根据判别式从而求实数b的值；
    （2）求出点A的坐标，因为圆A与抛物线C的准线相切，所以圆A的半径r等于圆心A到抛物线的准线y=-1的距离，问题得以解决．

    解答 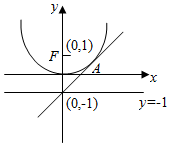解：（1）由$\left\{\begin{array}{l}y=x+b\\ x2=4y\end{array}$得x2-4x-4b=0，①
    因为直线l与抛物线C相切，所以△=（-4）2-4×（-4b）=0，
    解得b=-1．
    （2）由（1）可知b=-1，故方程①即为x2-4x+4=0，解得x=2，代入x2=4y，得y=1．
    故点A（2，1），
    因为圆A与抛物线C的准线相切，
    所以圆A的半径r等于圆心A到抛物线的准线y=-1的距离，即r=|1-（-1）|=2，
    所以圆A的方程为（x-2）2+（y-1）2=4．

    点评 本小题主要考查直线、圆、抛物线等基础知识，考查运算求解能力，考查函数与方程思想、数形结合思想．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．下列结论正确的是（　　）
    A．命题p：?x＞0，都有x2＞0，则?p：?x0≤0，使得x02≤0
    B．若命题p和p∨q都是真命题，则命题q也是真命题
    C．在△ABC中，a，b，c是角A，B，C的对边，则a＜b的充要条件是cosA＞cosB
    D．命题“若x2+x-2=0，则x=-2或x=1”的逆否命题是“x≠-2或x≠1，则x2+x-2≠0”

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．如图所示，已知在四棱锥P-ABCD中，底面ABCD为直角梯形，其中CD∥AB，AD⊥AB，侧棱PA⊥底面ABCD，且AD=DC=PA=$\frac{1}{2}$AB=1．
    （Ⅰ）求证：BC⊥平面PAC；
    （Ⅱ）设点M为PB中点，求四面体M-PAC的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知抛物线y2=ax的准线方程是x=-1，焦点为F．
    （1）求a的值；
    （2）过点F作直线交抛物线于A（x₁，y₁），B（x₂，y₂）两点，若x₁+x₂=6，求弦长AB．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．抛物线x2=4y上一点P到焦点的距离为3，则点P到y轴的距离为（　　）
    A．2$\sqrt{2}$B．1C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．如图，已知直线l与抛物线y2=2x相交于A（x1，y1），B（x2，y2）两点，与x轴相交于点M，若y1y2=-4，
    （1）求：M点的坐标；
    （2）求证：OA⊥OB；
    （3）求△AOB的面积的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．根据教材P45第6题可以证明函数g（x）=x2+ax+b满足性质$g（\frac{{{x_1}+{x_2}}}{2}）≤\frac{{g（{x_1}）+g（{x_2}）}}{2}$，理解其中的含义．对于函数f（x）=2x，h（x）=log2x及任意实数x1，x2，仿照上述理解，可以推测（　　）
    A．$f（\frac{{{x_1}+{x_2}}}{2}）≤\frac{{f（{x_1}）+f（{x_2}）}}{2}，h（\frac{{{x_1}+{x_2}}}{2}）≤\frac{{h（{x_1}）+h（{x_2}）}}{2}$
    B．$f（\frac{{{x_1}+{x_2}}}{2}）≥\frac{{f（{x_1}）+f（{x_2}）}}{2}，h（\frac{{{x_1}+{x_2}}}{2}）≥\frac{{h（{x_1}）+h（{x_2}）}}{2}$
    C．$f（\frac{{{x_1}+{x_2}}}{2}）≤\frac{{f（{x_1}）+f（{x_2}）}}{2}，h（\frac{{{x_1}+{x_2}}}{2}）≥\frac{{h（{x_1}）+h（{x_2}）}}{2}$
    D．$f（\frac{{{x_1}+{x_2}}}{2}）≥\frac{{f（{x_1}）+f（{x_2}）}}{2}，h（\frac{{{x_1}+{x_2}}}{2}）≤\frac{{h（{x_1}）+h（{x_2}）}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知抛物线C：y2=2px（p＞0）过点A（1，-2）
    （1）求抛物线C的方程，并求其焦点坐标；
    （2）是否存在平行于OA的直线（O为原点）L，使得直线L与抛物线C有公共点，且直线OA与L的距离等于$\frac{\sqrt{5}}{5}$？若存在，求出直线L的方程；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知抛物线的顶点在原点，对称轴为x轴，焦点在直线3x-4y-12=0上，那么抛物线通径长是16．

    查看答案和解析>>

    同步练习册答案