练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知二次函数f(x)的二次项系数为a，且f(x)>－2x的解集为{x|1<x<3}，方程f(x)＋6a＝0有两相等实根，求f(x)的解析式．


    解　设f(x)＋2x＝a(x－1)(x－3)(a<0)，

    则f(x)＝ax2－4ax＋3a－2x，

    f(x)＋6a＝ax2－(4a＋2)x＋9a，Δ＝(4a＋2)2－36a2＝0

    16a2＋16a＋4－36a2＝0,20a2－16a－4＝0

    5a2－4a－1＝0，(5a＋1)(a－1)＝0，

    解得a＝－，或a＝1舍去

    因此f(x)的解析式为f(x)＝－(x－1)(x－3)．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知p：∃x0∈R，mx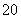＋2≤0.q：∀x∈R，x2－2mx＋1＞0，若p∨q为假命题，则实数m的取值范围是(　　)．

    A．[1，＋∞)                                       B．(－∞，－1]

    C．(－∞，－2]                                     D．[－1,1]

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知定义在R上的奇函数满足,且在区间上是增函数,则(     )

    A.          B.

    C.          D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知幂函数的图象经过点(2,4),则的解析式为(     )

    A.      B.      C.      D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数y＝mx2＋x＋5在[－2，＋∞)上是增函数，则m的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数y＝x3与y＝x－2的图象的交点为(x0，y0)，则x0所在的区间是(　　)．

    A．(0,1)                                    B．(1,2)

    C．(2,3)                                    D．(3,4)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝则f(log23)＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    生产一定数量的商品的全部费用称为生产成本，某企业一个月生产某种商品x万件时的生产成本为C(x)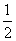＝x2＋2x＋20(万元)．一万件售价是20万元，为获取更大利润，该企业一个月应生产该商品数量为(　　)

    A．36万件                                           B．18万件

    C．22万件                                           D．9万件

    查看答案和解析>>

    同步练习册答案