练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数．

    （1）若，求证：；

    （2）若，，求的最大值；

    （3）求证：当时，．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2017届湖南长沙长郡中学高三上周测十二数学（文）试卷（解析版） 题型：解答题

    已知曲线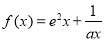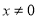（，）在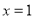处的切线与直线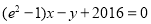平行．

    （1）讨论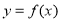的单调性；

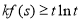    （2）若在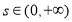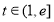，上恒成立，求实数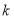的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．设函数g（x）=a（2x-1），h（x）=（2a2+1）1nx，其中a∈R．
    （Ⅰ）若直线x=2与曲线y=g（x）分别交于A、B两点，且曲线y=g（x）在点A处的切线与曲线y=h（x）在点B处的切线相互平行，求a的值；
    （Ⅱ）令f（x）=g（x）+h（x），若f（x）在[$\frac{1}{2}$，1]上没有零点，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．设函数f（x）=lnx-2x+6，则f（x）零点的个数为（　　）
    A．3B．2C．1D．0

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

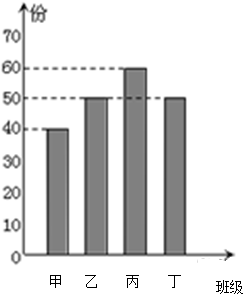    2．某研发公司研制出一款保护视力的护眼仪，并在新疆某中学的甲、乙、丙、丁四个班级中试用，这四个班级人数的条形图如下，为了了解学生护眼仪的使用情况，对四个班的学生进行了问卷调查，然后按分层抽样的方法从调查问卷中抽取20份进行统计，统计结果如下面表格所示：
     甲班 乙班 丙班 丁班
    满意  50% 80% 100% 60%
     一般 25% 0 0 0
     不满意 25% 20% 040%
    （1）若学生A在甲班，求学生A的调查问卷被选中的概率；
    （2）若需从调查问卷被选中且填写不满意的学生中再选2人进行访谈，求这两人中至少有一人是丁班学生的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知集合A={x|-5+21x-4x2＜0}，B={x∈Z|-3＜x＜6}，则（∁RA）∩B的元素的个数为（　　）
    A．3B．4C．5D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．以下是新兵训练时，某炮兵连8周中炮弹对同一目标的命中情况的柱状图：
     
    （1）计算该炮兵连这8周中总的命中频率p0，并确定第几周的命中频率最高；
    （2）以（1）中的p0作为该炮兵连炮兵甲对同一目标的命中率，若每次发射相互独立，且炮兵甲发射3次，记命中的次数为X，求X的数学期望；
    （3）以（1）中的p0作为该炮兵连炮兵对同一目标的命中率，试问至少要用多少枚这样的炮弹同时对该目标发射一次，才能使目标被击中的概率超过0.99？（取lg0.4=-0.398）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．给出下列结论：
    动点M（x，y）分别到两定点（-4，0），（4，0）连线的斜率之乘积为-$\frac{9}{16}$，设M（x，y）的轨迹为曲线C，F1、F2分别为曲线C的左右焦点，则下列命题中：
    （1）曲线C的焦点坐标为F1（-5，0），F2（5，0）；
    （2）曲线C上存在一点M，使得S△F1MF2=9；
    （3）P为曲线C上一点，P，F1，F2是直角三角形的三个顶点，且|PF1|＞|PF2|，$\frac{|P{F}_{1}|}{|P{F}_{2}|}$的值为$\frac{23}{9}$；
    （4）设A（1，1），动点P在曲线C上，则|PA|+|PF1|的最大值为8+$\sqrt{9-2\sqrt{7}}$；
    其中正确命题的序号是③④．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知一组数据a、b、9、10、11的平均数为10，方差为2，则|a-b|=（　　）
    A．2B．4C．8D．12

    查看答案和解析>>

    同步练习册答案