
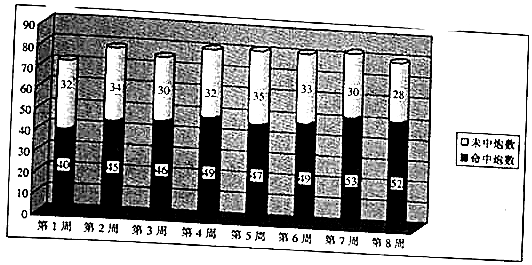
分析 (1)先求出这8周总总命中炮数和总未命中炮数,由此能求出该炮兵连这8周中总的命中频率,从而根据表中数据能求出第8周的命中率最高.
(2)由题意知X~B(3,0.6),由此能求出X的数学期望.
(3)由1-(1-P0)n>0.99,得0.4n<0.01,由此能求出至少要用6枚这样的炮弹同时对该目标发射一次,才能使目标被击中的概率超过0.99.
解答 解:(1)这8周总总命中炮数为:40+45+46+49+47+49+53+52=381,
总未命中炮数为32+34+30+32+35+33+30+28=254,
∴该炮兵连这8周中总的命中频率p0=$\frac{381}{381+254}=0.6$,
∵$\frac{52}{28}>\frac{53}{30}$,
∴根据表中数据知第8周的命中率最高.
(2)由题意知X~B(3,0.6),
则X的数学期望为E(X)=3×0.6=1.8.
(3)由1-(1-P0)n>0.99,解得0.4n<0.01,
∴n>log0.40.01=$\frac{lg0.01}{lg0.4}$=-$\frac{2}{lg0.4}$=$\frac{2}{0.398}$≈5.025,
∴至少要用6枚这样的炮弹同时对该目标发射一次,才能使目标被击中的概率超过0.99.
点评 本题考查频率的求法及应用,考查概率的求法及应用,是中档题,解题时要认真审题,注意二项分布的合理运用.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(文)试卷(解析版) 题型:选择题
已知函数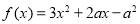 ,其中
,其中 ,
, 对任意的
对任意的 都成立,在1和
都成立,在1和 两数间插入2015个数,使之与1,
两数间插入2015个数,使之与1,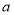 构成等比数列,设插入的这2015个数的成绩为
构成等比数列,设插入的这2015个数的成绩为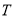 ,则
,则 ( )
( )
A. B.
B.
C. D.
D.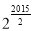
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
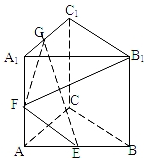 正三棱柱ABC-A1B1C1,E,F,G为 AB,AA1,A1C1的中点,则B1F与面GEF成角的正弦值( )
正三棱柱ABC-A1B1C1,E,F,G为 AB,AA1,A1C1的中点,则B1F与面GEF成角的正弦值( )| A. | $\frac{5}{6}$ | B. | $\frac{3}{5}$ | C. | $\frac{3\sqrt{3}}{10}$ | D. | $\frac{3\sqrt{6}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 椭圆 | B. | 三角形 | C. | 菱形 | D. | 两条平行线 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | [0,+∞) | C. | (1,+∞) | D. | ∅ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com