
���� ��1�����P������Ϊ��x��y������$|{\overrightarrow{PB}}|•|{\overrightarrow{BA}}|=\overrightarrow{PA}•\overrightarrow{BA}$��$\sqrt{{x^2}+{{��y-2��}^2}}=2+y$�����ɵó���
��2��������֪����AB'�ķ���Ϊy=kx-2���������߷���������Ϊ��x2-8kx+16=0����=0�����k��ֱ��AB�Ƶ�A��ʱ����ת$�ȣ�0���ȣ�\frac{��}{2}��$�õ�AB'�����ɵó���
��3�����E��F������ֱ�Ϊ��x1��y1������x2��y2�����ɣ�2��֪D��-4��2��������k1•k2=3���ɵ�$\frac{{{y_1}-2}}{{{x_1}+4}}•\frac{{{y_2}-2}}{{{x_2}+4}}=3$����E��F������C�ϣ�$x_1^2=8{y_1}��x_2^2=8{y_2}$������ʽ�����ã�x1x2-4��x1+x2��-176=0��ֱ��EF�ķ���Ϊ��$y=\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}��x-{x_1}��+{y_1}$�����뻯�ɵó���
��� �⣺��1�����P������Ϊ��x��y������$|{\overrightarrow{PB}}|•|{\overrightarrow{BA}}|=\overrightarrow{PA}•\overrightarrow{BA}$��$\sqrt{{x^2}+{{��y-2��}^2}}=2+y$��
�����x2=8y��������C�ķ�����x2=8y��
��2��������֪����AB'�ķ���Ϊy=kx-2��
��$\left\{{\begin{array}{l}{y=kx-2}\\{{x^2}=8y}\end{array}}\right.$��ȥy�ã�x2-8kx+16=0��������
���=64k2-64=0����k=��1��
��ֱ��AB�Ƶ�A��ʱ����ת$�ȣ�0���ȣ�\frac{��}{2}��$�õ�AB'��
��k=-1���루����ʽ���x=-4����y=2��
���D�������ǣ�-4��2����
��3�����E��F������ֱ�Ϊ��x1��y1������x2��y2�����ɣ�2��֪D��-4��2����
��k1•k2=3����$\frac{{{y_1}-2}}{{{x_1}+4}}•\frac{{{y_2}-2}}{{{x_2}+4}}=3$��
��E��F������C�ϣ���$x_1^2=8{y_1}��x_2^2=8{y_2}$������ʽ�����ã�x1x2-4��x1+x2��-176=0��
ֱ��EF�ķ���Ϊ��$y=\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}��x-{x_1}��+{y_1}$����$y=\frac{{{x_1}+{x_2}}}{8}��x-{x_1}��+\frac{x_1^2}{8}=\frac{{{x_1}+{x_2}}}{8}x-\frac{{{x_1}{x_2}}}{8}$��
��$y=\frac{{{x_1}+{x_2}}}{8}x-\frac{{4��{x_1}+{x_2}��+176}}{8}$����$y=\frac{{{x_1}+{x_2}}}{8}��x-4��-22$��
��ֱ��EF�����㣨4��-22��
���� ���⿼���������ߵı����̼������ʡ�б�ʼ��㹫ʽ��ֱ�߷��̡�����֮��ľ��빫ʽ����������������������������������⣮


 ��Ȥ����¹�֪��ϵ�д�
��Ȥ����¹�֪��ϵ�д� Ӣ��СӢ������Ĭдϵ�д�
Ӣ��СӢ������Ĭдϵ�д� �����ҵ���������ͯ������ϵ�д�
�����ҵ���������ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | -5��5 | C�� | 1 | D�� | 1��-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
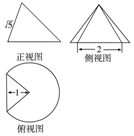 һ��Բ���������ƽ���ȥ�˽�С��һ���֣����µļ����������ͼ��ͼ����ü���������Ϊ��������
һ��Բ���������ƽ���ȥ�˽�С��һ���֣����µļ����������ͼ��ͼ����ü���������Ϊ��������| A�� | $��+\frac{2}{3}$ | B�� | $��+\frac{1}{3}$ | C�� | $\frac{3}{4}��+\frac{2}{3}$ | D�� | $\frac{3}{4}��+\frac{1}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
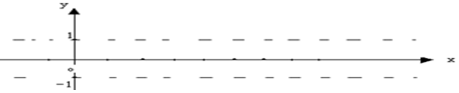
| x | |||||
| $\frac{1}{2}$x+$\frac{��}{6}$ | |||||
| y |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��2016��+�ޣ� | B�� | ��-�ޣ�0���ȣ�2016��+�ޣ� | C�� | ��-�ޣ�0���ȣ�0��+�ޣ� | D�� | ��0��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $x=��\frac{{\sqrt{3}}}{3}y$ | B�� | $y=��\frac{{\sqrt{3}}}{3}x$ | C�� | $y=��\frac{{\sqrt{3}}}{2}x$ | D�� | $x=��\frac{{\sqrt{3}}}{2}y$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com