
分析 ①由sin$\frac{α}{2}$+cos$\frac{α}{2}$=$\sqrt{2}$sin($\frac{α}{2}$+$\frac{π}{4}$)≤$\sqrt{2}$<$\frac{3}{2}$,判断①错;
②由函数y=sin(2x+$\frac{3π}{2}$)=-cos2x是偶函数,判断②正确;
③求出函数y=|tan(2x+$\frac{π}{4}$)|的周期为$\frac{π}{2}$,判断③正确;
④举例说明该命题错误;
⑤求出函数y的最大值,判断⑤错误.
解答 解:对于①,sin$\frac{α}{2}$+cos$\frac{α}{2}$=$\sqrt{2}$sin($\frac{α}{2}$+$\frac{π}{4}$)≤$\sqrt{2}$<$\frac{3}{2}$,
∴存在实数α,使sin$\frac{α}{2}$+cos$\frac{α}{2}$=$\frac{3}{2}$是假命题,故①错误;
对于②,函数y=sin(2x+$\frac{3π}{2}$)=-cos2x,是定义域R上的偶函数,故②正确;
对于③,函数y=|tan(2x+$\frac{π}{4}$)|的周期为T=$\frac{π}{ω}$=$\frac{π}{2}$,故③正确;
对于④,当α=$\frac{9π}{4}$、β=$\frac{π}{4}$时,α、β是第一象限的角,且α>β,但sinα=sinβ=$\frac{\sqrt{2}}{2}$,故④错误;
对于⑤,函数y═sin2x-3cosx+2=-cos2x-3cosx+3=-${(cosx+\frac{3}{2})}^{2}$+$\frac{21}{4}$,
当cosx=-1时,y取得最大值为5,故⑤错误.
其中正确命题的是②③.
故答案为:②③.
点评 本题考查了三角函数的图象与性质的应用问题,也考查了三角函数的化简与求值问题,是综合性题目.


科目:高中数学 来源: 题型:解答题
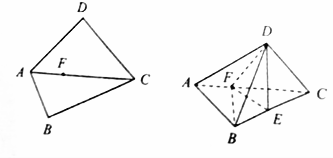 如图,平面四边形ABCD中,∠B=∠D=90°,AC=2AB=4$\sqrt{3}$,DA=DC,F是AC上一点,且AF=$\frac{1}{3}$AC.将该四边形沿AC折起,使点D在平面ABC的射影E恰在BC上,此时DE=2$\sqrt{2}$.
如图,平面四边形ABCD中,∠B=∠D=90°,AC=2AB=4$\sqrt{3}$,DA=DC,F是AC上一点,且AF=$\frac{1}{3}$AC.将该四边形沿AC折起,使点D在平面ABC的射影E恰在BC上,此时DE=2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2) | B. | (-2,-1] | C. | (-2,-1) | D. | (2,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com