
分析 (1)先求导,再分类讨论求出f(x)的单调区间;
(2)若定义域内存在三个不同的自变量的取值xi(i=1,2,3),使得f(xi)-g(xi)的值恰好都相等,设f(xi)-g(xi)=m.(i=1,2,3),则对于某一实数m,方程f(x)-g(x)=m在(0,+∞)上有三个不等的实数,由此能求出在定义域内不存在三个不同的自变量的取值xi(i=1,2,3)使得f(xi)-g(xi)的值恰好都相等.
解答 解:(1)f(x)=$\frac{1}{3}$x3-x2+ax,
∴f′(x)=x2-2x+a,
当△=4-4a≤0时,即a≥1时,f′(x)≥0恒成立,
∴f(x)在(0,+∞)上的单调递增,
当△=4-4a>0时,即a<1时,
令f′(x)=0,解得x=1-$\sqrt{1-a}$或x=1+$\sqrt{1-a}$,
当1-$\sqrt{1-a}$≤0时,即a≤0时,f(x)在(0,1+$\sqrt{1-a}$)上单调递减,在(1+$\sqrt{1-a}$,+∞)上单调递增,
当1-$\sqrt{1-a}$>0时,即0<a<1时,f(x)在(1-$\sqrt{1-a}$,1+$\sqrt{1-a}$)上单调递减,在(0,1-$\sqrt{1-a}$),(1+$\sqrt{1-a}$,+∞)上单调递增.
(Ⅱ)若存在,设f(xi)-g(xi)=m(i=1,2,3),
则对于某一实数m方程f(x)-g(x)-m=0在(0,+∞)上有三个不等的实根,
设F(x)=f(x)-g(x)-m=$\frac{1}{3}$x3-x2+ax-$\frac{1}{3}$x3-(a-1)x+alnx-m=-x2+x+alnx+m,
则函数F(x)=f(x)+g(x)-m的图象与x轴有三个不同交点,
即F′(x)=-2x+1+$\frac{a}{x}$=$\frac{-2{x}^{2}+x+a}{x}$在(0,+∞)有两个不同的零点,
令h(x)=-2x2+x+a=0有两个不相等的正实数根,设两个根为x1,x2,
∴△=1+4×2a>0,且x1•x2=-$\frac{a}{2}$>0,
解得-$\frac{1}{8}$<a<0,
∴a的取值范围为(-$\frac{1}{8}$,0).
点评 本题考查函数的单调区间的求法,考查满足条件的实数的取值范围的求法.综合性强,难度大,具有一定的探索性.解题时要认真审题,仔细解答,注意合理地进行等价转化.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:解答题
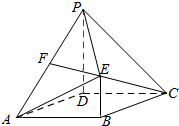 如图,四边形ABCD是菱形,PD⊥平面ABCD,PD∥BE,AD=PD=2BE=2,∠DAB=60°,点F为PA的中点.
如图,四边形ABCD是菱形,PD⊥平面ABCD,PD∥BE,AD=PD=2BE=2,∠DAB=60°,点F为PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
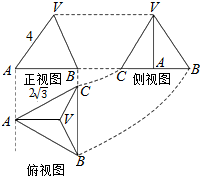
| A. | $\sqrt{39}$ | B. | 6$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)中,F1,F2分别是椭圆的左右焦点,点B(0,-b)是椭圆C的下顶点,BF1的延长线交椭圆C于点A,点D和点A关于x轴对称.
如图所示,在椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)中,F1,F2分别是椭圆的左右焦点,点B(0,-b)是椭圆C的下顶点,BF1的延长线交椭圆C于点A,点D和点A关于x轴对称.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
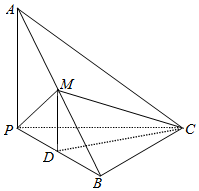 如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com