
分析 (1)设h(x)=lnx+$\frac{1}{2}$x2-2x+$\frac{3}{2}$,x∈(1,+∞),求出函数的导数,判断导函数的符号,推出结果.
(2)不妨设h(x)=f(x)-g(x)=lnx+k(x-1)2-x+1,x∈(1,+∞),求出函数的导数,①当k≤0时,判断函数的单调性,推出结果;②当$0<k<\frac{1}{2}$时,③当k$≥\frac{1}{2}$时,判断导函数的单调性,求出函数的最值,推出实数k的取值范围.
解答 (本小题满分12分)
解:(1)当k=$\frac{1}{2}$时,设h(x)=f(x)-g(x)=lnx+$\frac{1}{2}$(x-1)2-x+1,x∈(1,+∞),
h(x)=lnx+$\frac{1}{2}$x2-2x+$\frac{3}{2}$,x∈(1,+∞)
h′(x)=$\frac{1}{x}$+x-2=$\frac{{x}^{2}-2x+1}{x}$=$\frac{({x-1)}^{2}}{x}$,
∵x>1,h′(x)>0,∴h(x)在(1,+∞)上单调递增,h(x)>h(1)=0恒成立
∴当k=$\frac{1}{2}$,x∈(1,+∞)时,f(x)>g(x)恒成立
(2)不妨设h(x)=f(x)-g(x)=lnx+k(x-1)2-x+1,x∈(1,+∞)
h(x)=lnx+kx2-(2k+1)x+k+1,x∈(1,+∞)
h′(x)=$\frac{1}{x}$+2kx-(2k+1)=$\frac{2k{x}^{2}-(2k+1)x+1}{x}$=$\frac{(2kx-1)(x-1)}{x}$,
∵x>1,∴$\frac{x-1}{x}>0$,
①当k≤0时,2kx-1<0,
∴h′(x)<0,∴h(x)在(1,+∞)上单调递减,
∴h(x)<h(1)=0,不合题意,舍
②当$0<k<\frac{1}{2}$时,由h′(x)>0可得x<1或x$>\frac{1}{2k}$,由h′(x)<0可得1$<x<\frac{1}{2k}$,
∴h(x)在(1,$\frac{1}{2k}$)上单调递减,在[$\frac{1}{2k}$,+∞)上单调递增
∴?x∈(1,$\frac{1}{2k}$),都有h(x)<h(1)=0,不合题意,舍
③当k$≥\frac{1}{2}$时,由h′(x)>0可得x>1或x$<\frac{1}{2k}$,由h′(x)<0可得$\frac{1}{2k}<x<1$,
∴h(x)在(1,+∞)上单调递增,∴h(x)>h(1)=0恒成立
综上所述,实数k的取值范围是[$\frac{1}{2}$,+∞).
点评 本题考查函数的导数的应用,单调性以及函数的最值的求法,考查函数恒成立的应用,转化思想以及计算能力.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
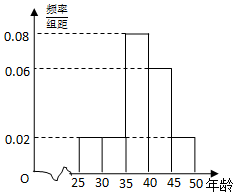 某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图:
某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图:| 区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
| 人数 | 50 | 50 | a | 150 | b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com