练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．等差数列{an}的前m项和为30，前3m项和为90，则它的前2m项和为60．

    分析 根据题意和等差数列的前n项和性质得，30、S2m-30、90-S2m成等差数列，由等差中项的性质列出方程，再求出它的前2m项和的值．

    解答 解：设Sn是等差数列{an}的前n项和，
    所以Sm、S2m-Sm、S3m-S2m成等差数列，
    即30、S2m-30、90-S2m成等差数列，
    所以2（S2m-30）=30+90-S2m，解得S2m=60，
    故答案为：60．

    点评 本题考查等差数列的前n项和性质，以及等差中项的性质的应用，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    17．若$\sqrt{3}$是3a与3b的等比中项，则a+b的值为（　　）
    A．-1B．0C．1D．$\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．设x∈R，则“log2x＜1”是“x2-x-2＜0”的充分不必要条件．（从“充分不必要”、“必要不充分”、“既不充分也不必要”、“充要”中选择）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．在三角形ABC中，角A，B，C所对的边分别是a，b，c．已知b=3，c=2．
    （1）若2a•cosC=3，求a的值；
    （2）若$\frac{c}{b}=\frac{cosC}{1+cosB}$，求cosC的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．圆（x-1）2+（y-2）2=5的圆心坐标是（1，2）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

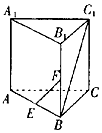    12．如图所示，在直三棱柱ABC-A1B1C1中，AB=AA1=2，∠ABC=90°，点E、F分别是棱AB、BB1的中点，当二面角C1-AA1-B为45o时，直线EF和BC1所成的角为（　　）
    A．45oB．60oC．90oD．120o

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．给出下列命题：
    ①点P（-1，4）到直线3x+4y=2的距离为3．
    ②过点M（-3，5）且在两坐标轴上的截距互为相反数的直线方程为x-y+8=0．
    ③命题“?x∈R，使得x2-2x+1＜0”的否定是真命题；
    ④“x≤1，且y≤1”是“x+y≤2”的充要条件．
    其中不正确命题的序号是①②④．（把你认为不正确命题的序号都填上）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．下列四个命题中错误的是（　　）
    A．在一次试卷分析中，从每个考室中抽取第5号考生的成绩进行统计，不是简单随机抽样
    B．对一个样本容量为100的数据分组，各组的频数如下：
    区间[17，19）[19，21）[21，23）[23，25）[25，27）[27，29）[29，31）[31，33]
    频数113318162830
    估计小于29的数据大约占总体的58%
    C．设产品产量与产品质量之间的线性相关系数为-0.91，这说明二者存在着高度相关
    D．通过随机询问110名性别不同的行人，对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查，得到如表列联表：
    男女总计
    走天桥402060
    走斑马线203050
    总计6050110
    由${K^2}=\frac{{110×{{（40×30-20×20）}^2}}}{60×50×60×50}=7.8$，则有99%以上的把握认为“选择过马路方式与性别有关”

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．在△ABC中，已知|BC|=4，且$\frac{{|{AB}|}}{{|{AC}|}}=λ$，求点A的轨迹方程，并说明轨迹是什么图形．

    查看答案和解析>>

    同步练习册答案