Question

6．某市一路公共汽车每天早晨在6：20-6：40内任何时刻随机的发出第一班车，在6：40-7：00内任何时刻随机的发出第二班车，在7：00-7：20内任何时刻随机的发出第三班车，老张每天早晨在6：20-7：20内任意时刻都等可能的到一路公共汽车的起点站乘车上班（假设老张上班只乘坐一路公共汽车），则老张乘一路公共汽车前三班的概率是$\frac{5}{6}$．

Answer 1

分析 设汽车在7：00-7：20发车为变量x，老张在7：00-7：20达到为变量y，要使老张乘1路公共汽车前3班车，只要x≤y，画出图形，求出面积，利用几何概型公式解答．

解答 解：设汽车在7：00-7：20发车为变量x，老张在7：00-7：20达到为变量y，
要使老张乘1路公共汽车前3班车，只要x≤y，
如图示：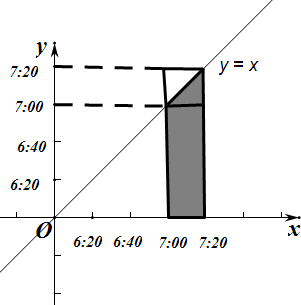
，
满足条件的如图阴影部分，
∴老张乘1路公共汽车前3班车的概率为1-$\frac{\frac{1}{2}×20×20}{20×60}$=$\frac{5}{6}$，
故答案为：$\frac{5}{6}$．

点评 本题考查了几何概型的运用；关键是明确老张乘1路公共汽车前3班车与汽车达到的时间的关系，分别求出面积，利用几何概型公式解答．