
| A. | [$\sqrt{2}$,+∞) | B. | [2$\sqrt{2}$,+∞) | C. | [$\frac{\sqrt{6}}{6}$,+∞) | D. | (-∞,0] |
分析 联立$\left\{\begin{array}{l}{\frac{x}{a}+\frac{y}{b}=m}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,化为:2x2-2amx+a2(m2-1)=0,根据?M∈P,M∉Q,可得△≤0,解出实数m的取值范围即可.
解答 解:联立$\left\{\begin{array}{l}{\frac{x}{a}+\frac{y}{b}=m}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,化为:2x2-2amx+a2(m2-1)=0,
∵?M∈P,M∉Q,∴△=4a2m2-8a2(m2-1)≤0,
解得:$m≥\sqrt{2}$.
∴实数m的取值范围是$[\sqrt{2},+∞)$.
故选:A.
点评 本题考查了椭圆的标准方程及其性质、不等式的性质、直线与椭圆的位置关系,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | -1或1 | D. | 0或2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cos(-$\frac{π}{10}$)<cos(-$\frac{π}{9}$) | B. | tan$\frac{π}{6}$<tan$\frac{2}{7}$π | C. | sin$\frac{8}{7}$π>sin$\frac{π}{11}$ | D. | cos$\frac{2}{5}$π<cos$\frac{6}{5}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
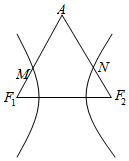 (普通中学做)如图,已知F1、F2为双曲线的两焦点,等边三角形AF1F2两边的中点M、N在双曲线上,则该双曲线的离心率为( )
(普通中学做)如图,已知F1、F2为双曲线的两焦点,等边三角形AF1F2两边的中点M、N在双曲线上,则该双曲线的离心率为( )| A. | $\sqrt{3}$+1 | B. | $\sqrt{2}$+1 | C. | $\sqrt{5}$+1 | D. | $\sqrt{5}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com