练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．如图，在边长为2的正六边形ABCDEF中，则$\overrightarrow{AB}•\overrightarrow{CD}$=-2．

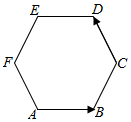
    分析 根据图形，$\overrightarrow{AB}•\overrightarrow{CD}=\overrightarrow{ED}•\overrightarrow{CD}$，而$＜\overrightarrow{ED}，\overrightarrow{CD}＞=120°$，且$|\overrightarrow{ED}|=2，|\overrightarrow{CD}|=2$，这样即可求出$\overrightarrow{ED}•\overrightarrow{CD}$的值，即得出$\overrightarrow{AB}•\overrightarrow{CD}$的值．

    解答 解：$\overrightarrow{AB}•\overrightarrow{CD}=\overrightarrow{ED}•\overrightarrow{CD}$=$|\overrightarrow{ED}||\overrightarrow{CD}|cos＜\overrightarrow{ED}，\overrightarrow{CD}＞$=2•2cos120°=-2．
    故答案为：-2．

    点评 考查正六边形的内角为120°，以及相对的边平行，相等向量的概念，数量积的计算公式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

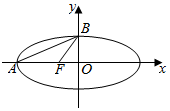    12．如图，在平面直角坐标系xOy中，已知椭圆$\frac{{x}^{2}}{a}$+y2=1（a＞1）的左顶点为A，左焦点为F，上顶点为B，若∠BAO+∠BFO=90°，则a的值为（　　）
    A．$\frac{\sqrt{5}-1}{2}$B．$\frac{1+\sqrt{5}}{2}$C．$\sqrt{\frac{1+\sqrt{5}}{2}}$D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知复数z=（$\frac{1+i}{1-i}$）2016+（1-i）2（其中i为虚数单位）．若复数z的共扼复数为$\overline{z}$，且$\overline{z}$•z1=4+3i．
    （1）求复数z1及z1在复平面中对应点的坐标；
    （2）若z1是关于x的方程x2-px+q=0的一个根，求实数p，q的值，并求出方程x2-px+q=0的另一个复数根．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．己知x0=$\frac{π}{3}$是函数f（x）=sin（2x+φ）的一个极大值点，则f（x）的一个单调递减区间是（　　）
    A．（$\frac{π}{6}$，$\frac{2π}{3}$）B．（$\frac{π}{3}$，$\frac{5π}{6}$）C．（$\frac{π}{2}$，π）D．（$\frac{2π}{3}$，π）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知函数f（x）=sin（x-$\frac{π}{6}$）cos（x-$\frac{π}{6}$）（x∈R），则下列结论错误的是（　　）
    A．函数f（x）的最小正周期为πB．函数f（x）的图象关于直线x=-$\frac{π}{12}$对称
    C．函数f（x）的图象关于点（-$\frac{π}{6}$，0）对称D．函数f（x）在区间[0，$\frac{5π}{12}$]上是增函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．已知x，y满足$\left\{\begin{array}{l}y≥x\\ x+y≤2\\ x≥a\end{array}\right.$，且z=2x-y的最大值是最小值的-2倍，则a的值是$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．在△ABC中，内角A、B、C所对应的边分别为a、b、c，且（a+b+c）（a+b-c）=3ab．
    （Ⅰ）求角C；
    （Ⅱ）f（x）=$\sqrt{3}sin（{2x-\frac{C}{2}}）+2{sin^2}（{x-\frac{π}{12}}）$在区间$[{0，\frac{π}{2}}]$上的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知函数f（x）的导函数f′（x）=2+sinx，且f（0）=-1，数列{an}是以$\frac{π}{4}$为公差的等差数列，若f（a2）+f（a3）+f（a4）=3π，则$\frac{{a}_{2016}}{{a}_{2}}$=（　　）
    A．2016B．2015C．2014D．2013

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知函数$f（x）=2sinωxcos（ωx+\frac{π}{3}）$（ω＞0）的最小正周期为π．
    （Ⅰ）求ω的值；
    （Ⅱ）求f（x）在区间$[-\frac{π}{6}，\frac{π}{2}]$上的最大值和最小值．

    查看答案和解析>>

    同步练习册答案