
(本小题满分12分)已知函数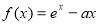 (
(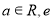 为自然对数的底数).
为自然对数的底数).
(Ⅰ)讨论函数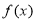 的单调性;
的单调性;
(Ⅱ)若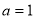 ,函数
,函数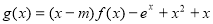 在
在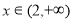 上为增函数,求实数
上为增函数,求实数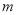 的取值范围.
的取值范围.
(1)当 时,所以
时,所以 在
在 上为增函数,当
上为增函数,当 时,函数
时,函数 在
在 上为减函数,
上为减函数,
所以函数 在
在 上为增函数;(2)
上为增函数;(2) .
.
【解析】
试题分析:(1)函数 在某个区间内可导,则若
在某个区间内可导,则若 ,则
,则 在这个区间内单调递增,若
在这个区间内单调递增,若 ,则
,则 在这个区间内单调递减;(2)若可导函数
在这个区间内单调递减;(2)若可导函数 在指定的区间
在指定的区间 上单调递增(减),求参数问题,可转化为
上单调递增(减),求参数问题,可转化为
 恒成立,从而构建不等式,要注意“=”是否可以取到;(3)对于恒成立的问题,常用到两个结论:(1)
恒成立,从而构建不等式,要注意“=”是否可以取到;(3)对于恒成立的问题,常用到两个结论:(1) 恒成立
恒成立 ,(2)
,(2) 恒成立
恒成立 ;(4)利用导数方法证明不等式
;(4)利用导数方法证明不等式 在区间
在区间 上恒成立的基本方法是构造函数
上恒成立的基本方法是构造函数 ,然后根据函数的单调性,或者函数的最值证明函数
,然后根据函数的单调性,或者函数的最值证明函数 ,其中一个重要的技巧就是找到函数
,其中一个重要的技巧就是找到函数 在什么地方可以等于零,这往往就是解决问题的一个突破口,观察式子的特点,找到特点证明不等式.
在什么地方可以等于零,这往往就是解决问题的一个突破口,观察式子的特点,找到特点证明不等式.
试题解析:(Ⅰ)函数 的定义域为
的定义域为

当 时,
时, ,所以
,所以 在
在 上为增函数;
上为增函数;
当 时,由
时,由 得
得
则:当 时,
时, ,所以函数
,所以函数 在
在 上为减函数,
上为减函数,
当 时,
时, ,
,
所以函数 在
在 上为增函数. 6分
上为增函数. 6分
(Ⅱ)当 时,
时, ,
,
∵ 在
在 上为增函数,
上为增函数,

 在
在 恒成立,
恒成立,
即 在
在 恒成立,
恒成立,
令 ,
, ,
,
 ,
,
令 ,
,
 在
在 恒成立,
恒成立,
即 在
在 单调递增,
单调递增,
即 ,
,

即 在
在 单调递增,
单调递增,

所以 . 12分
. 12分
考点:1、利用导数求函数的单调区间;2、函数单调性的应用;3、恒成立的问题.
考点分析: 考点1:导数及其应用 试题属性

科目:高中数学 来源:2014-2015学年吉林省长春市高三上学期阶段性考试文科数学试卷(解析版) 题型:选择题
在等差数列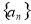 中,
中, 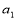 ,
,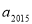 为方程
为方程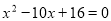 的两根,则
的两根,则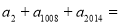 ( )
( )
A.10 B.15 C.20 D.40
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省汕头市高三第一次模拟考试文科数学试卷(解析版) 题型:选择题
下列函数中,是偶函数,且在区间 内单调递增的函数是( )
内单调递增的函数是( )
A. B.
B. C.
C.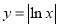 D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省兰州市高三诊断考试文科数学试卷(解析版) 题型:填空题
若函数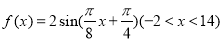 的图象与
的图象与 轴交于点
轴交于点 ,过点
,过点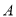 的直线
的直线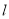 与函数
与函数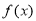 的图象交于
的图象交于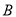 、
、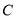 两点,
两点,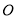 为坐标原点,则
为坐标原点,则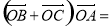 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省兰州市高三诊断考试文科数学试卷(解析版) 题型:选择题
已知不等式组 所表示的平面区域为
所表示的平面区域为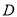 ,若直线
,若直线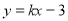 与平面区域
与平面区域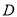 有公共点,则
有公共点,则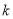 的取值范围为是
的取值范围为是
A.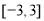
B.
C.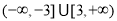
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省高三第一次联考理科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4—4:坐标系与参数方程
在直角坐标系 中,圆
中,圆 的参数方程
的参数方程 为参数).以
为参数).以 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求圆 的极坐标方程;
的极坐标方程;
(2)直线 的极坐标方程是
的极坐标方程是 ,射线
,射线 与圆
与圆 的交点为
的交点为 ,与直线
,与直线 的交点为
的交点为 ,求线段
,求线段 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com