
【题目】关于复数![]() ,下列命题①若
,下列命题①若![]() ,则
,则![]() ;②
;②![]() 为实数的充要条件是
为实数的充要条件是![]() ;③若
;③若![]() 是纯虚数,则
是纯虚数,则![]() ;④若
;④若![]() ,则
,则![]() .其中真命题的个数为( )
.其中真命题的个数为( )
A.1B.2
C.3D.4
科目:高中数学 来源: 题型:
【题目】将数列![]() 的前n项和分成两部分,且两部分的项数分别是i,
的前n项和分成两部分,且两部分的项数分别是i,![]() ,若两部分的和相等,则称数列
,若两部分的和相等,则称数列![]() 的前n项和能够进行
的前n项和能够进行![]() 等和分割.
等和分割.
![]() 若
若![]() ,
,![]() ,试写出数列
,试写出数列![]() 的前4项和的所有等和分割;
的前4项和的所有等和分割;
![]() 求证:等差数列
求证:等差数列![]() 的前
的前![]() 项和能够进行
项和能够进行![]() 等和分割;
等和分割;
![]() 若数列
若数列![]() 的通项公式为:
的通项公式为:![]() ,且数列
,且数列![]() 的前n项和能进行等和分割,求所有满足条件的n.
的前n项和能进行等和分割,求所有满足条件的n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已如椭圆C:![]() 的两个焦点与其中一个顶点构成一个斜边长为4的等腰直角三角形.
的两个焦点与其中一个顶点构成一个斜边长为4的等腰直角三角形.
(1)求椭圆C的标准方程;
(2)设动直线l交椭圆C于P,Q两点,直线OP,OQ的斜率分别为k,k'.若![]() ,求证△OPQ的面积为定值,并求此定值.
,求证△OPQ的面积为定值,并求此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某群体的人均通勤时间,是指单日内该群体中成员从居住地到工作地的平均用时.某地上班族![]() 中的成员仅以自驾或公交方式通勤.分析显示:当
中的成员仅以自驾或公交方式通勤.分析显示:当![]() 中
中![]() (
(![]() )的成员自驾时,自驾群体的人均通勤时间为
)的成员自驾时,自驾群体的人均通勤时间为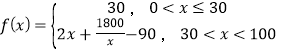 (单位:分钟),而公交群体的人均通勤时间不受
(单位:分钟),而公交群体的人均通勤时间不受![]() 影响,恒为
影响,恒为![]() 分钟,试根据上述分析结果回答下列问题:
分钟,试根据上述分析结果回答下列问题:
(1)当![]() 在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
(2)求该地上班族![]() 的人均通勤时间
的人均通勤时间![]() 的表达式;讨论
的表达式;讨论![]() 的单调性,并说明其实际意义.
的单调性,并说明其实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为F1,F2,该椭圆与y轴正半轴交于点M,且△MF1F2是边长为2的等边三角形.
的左右焦点分别为F1,F2,该椭圆与y轴正半轴交于点M,且△MF1F2是边长为2的等边三角形.
(1)求椭圆的标准方程;
(2)过点F2任作一直线交椭圆于A,B两点,平面上有一动点P,设直线PA,PF2,PB的斜率分别为k1,k,k2,且满足k1+k2=2k,求动点P的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某公园有三条观光大道![]() 、
、![]() 、
、![]() 围成直角三角形,其中直角边
围成直角三角形,其中直角边![]() ,斜边
,斜边![]() .
.

(1)若甲乙都以每分钟100![]() 的速度从点
的速度从点![]() 出发,甲沿
出发,甲沿![]() 运动,乙沿
运动,乙沿![]() 运动,乙比甲迟2分钟出发,求乙出发后的第1分钟末甲乙之间的距离;
运动,乙比甲迟2分钟出发,求乙出发后的第1分钟末甲乙之间的距离;
(2)现有甲、乙、丙三位小朋友分别在点![]() 、
、![]() 、
、![]() ,设
,设![]() ,乙丙之间的距离
,乙丙之间的距离![]() 是甲乙之间距离
是甲乙之间距离![]() 的2倍,且
的2倍,且![]() ,请将甲乙之间的距离
,请将甲乙之间的距离![]() 表示为
表示为![]() 的函数,并求甲乙之间的最小距离.
的函数,并求甲乙之间的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合![]() 是实数集
是实数集![]() 的子集,如果正实数
的子集,如果正实数![]() 满足:对任意
满足:对任意![]() 都存在
都存在![]() 使得
使得![]() 则称
则称![]() 为集合
为集合![]() 的一个“跨度”,已知三个命题:
的一个“跨度”,已知三个命题:
(1)若![]() 为集合
为集合![]() 的“跨度”,则
的“跨度”,则![]() 也是集合
也是集合![]() 的“跨度”;
的“跨度”;
(2)集合![]() 的“跨度”的最大值是4;
的“跨度”的最大值是4;
(3)![]() 是集合
是集合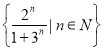 的“跨度”.
的“跨度”.
这三个命题中正确的个数是()
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com