
| A. | (1,$\frac{3}{2}$) | B. | (0,$\frac{3}{2}$) | C. | (1,$\frac{5}{2}$) | D. | (0,$\frac{5}{2}$) |
分析 可设P为双曲线的右支上一点,|PF1|=m,|PF2|=n,运用双曲线的定义和P在右支上,有n>c-a,结合不等式的性质和离心率公式计算即可得到所求范围.
解答 解:可设P为双曲线的右支上一点,
|PF1|=m,|PF2|=n,
由双曲线的定义可得m-n=2a,
由题意可得m+n+2c=6a,
即有2n+2a+2c=6a,
即n=2a-c,
再由P在右支上,可得n>c-a,
即有2a-c>c-a,即c<$\frac{3}{2}$a,
由e=$\frac{c}{a}$,可得1<e<$\frac{3}{2}$.
故选:A.
点评 本题考查双曲线的离心率的范围,注意运用双曲线的定义和性质,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 128 | B. | $\frac{128}{3}$ | C. | $\frac{64}{3}$ | D. | $\frac{32}{3}$ |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年山西忻州一中高一上学期新生摸底数学试卷(解析版) 题型:解答题
如图,在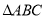 中,
中,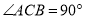 ,
,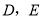 分别为
分别为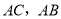 的中点,
的中点,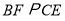 交
交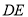 的延长线于点
的延长线于点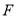 .
.

(1)求证:四边形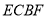 是平行四边形;
是平行四边形;
(2)当 时,求证:四边形
时,求证:四边形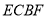 是菱形.
是菱形.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin(x+$\frac{π}{2}$) | B. | y=-cos4x | C. | y=-x2 | D. | y=|sin(π+x)| |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com