
分析 (1)运用正弦定理和三角形的内角和定理可得cosB,即可得sinB的值.
(2)由BD=1,运用向量的关系可得|$\overrightarrow{BA}+\overrightarrow{BC}$|=2|$\overrightarrow{BD}$|=2,平方后,可得|$\overrightarrow{BA}$|2+|$\overrightarrow{BC}$|2+2$\overrightarrow{BA}•\overrightarrow{BC}$=4利用基本不等式即可求解△ABD面积的最大值.
解答 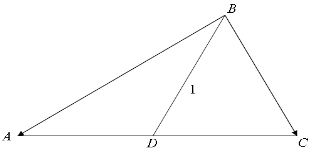 解:(1)由$\frac{b}{a}cosC=({3-\frac{c}{a}})cosB$.
解:(1)由$\frac{b}{a}cosC=({3-\frac{c}{a}})cosB$.
可得:$\frac{b}{a}cosC+\frac{c}{a}cosB=3cosB$
由正弦定理:$\frac{sinBcosC+sinCcosB}{sinA}=3cosB$.
得:$\frac{sinA}{sinA}=3cosB$.即cosB=$\frac{1}{3}$.
那么:sinB=$\frac{2\sqrt{2}}{3}$.
(2)由BD=1,运用向量的关系,可得|$\overrightarrow{BA}+\overrightarrow{BC}$|=2|$\overrightarrow{BD}$|=2,
可得:|$\overrightarrow{BA}$|2+|$\overrightarrow{BC}$|2+2$\overrightarrow{BA}•\overrightarrow{BC}$=4,
则|$\overrightarrow{BA}$|2+|$\overrightarrow{BC}$|2+2|$\overrightarrow{BA}|•|\overrightarrow{BC}$|cosB=4,
由余弦定理:得|$\overrightarrow{BA}$|2+|$\overrightarrow{BC}$|2=4-$\frac{2}{3}$×|$\overrightarrow{BA}|•|\overrightarrow{BC}$|
∵|$\overrightarrow{BA}$|2+|$\overrightarrow{BC}$|2≥2|$\overrightarrow{BA}$|•|$\overrightarrow{BC}$|,(当且仅当|$\overrightarrow{BA}$|=|$\overrightarrow{BC}$|时取等号)
∴4-$\frac{2}{3}$×|$\overrightarrow{BA}|•|\overrightarrow{BC}$|≥2|$\overrightarrow{BA}$|•|$\overrightarrow{BC}$|,
∴|$\overrightarrow{BA}$|•|$\overrightarrow{BC}$|≤$\frac{3}{2}$.
∴△ABC面积S=$\frac{1}{2}$|$\overrightarrow{BA}$|•|$\overrightarrow{BC}$|sinB≤$\frac{1}{2}×\frac{3}{2}×\frac{2\sqrt{2}}{3}$=$\frac{\sqrt{2}}{2}$
那么:△ABD面积的最大值为$\frac{\sqrt{2}}{2}×\frac{1}{2}$=$\frac{\sqrt{2}}{4}$.
点评 本题考查三角形的正余弦定理和内角和定理的运用,基本不等式的灵活运用,考查运算能力,属于中档题.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{2}i$ | B. | $\frac{1}{2}i$ | C. | $-\frac{3}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
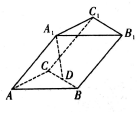 如图,在三棱柱ABC-A1B1C1中,底面ABC是边长为2的等边三角形,点A1在底面ABC上的投影D恰好为BC的中点,AA1与平面ABC所成角为45°,则该三棱柱的体积为( )
如图,在三棱柱ABC-A1B1C1中,底面ABC是边长为2的等边三角形,点A1在底面ABC上的投影D恰好为BC的中点,AA1与平面ABC所成角为45°,则该三棱柱的体积为( )| A. | 1 | B. | $\sqrt{2}$ | C. | 3 | D. | $\sqrt{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com