
分析 以AB为x轴,以AB的中垂线为y轴建立平面坐标系,求出C(1,$\sqrt{3}$),设双曲线方程为$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1,计算当x=1时对于的y值,令y≥$\sqrt{3}$即可.
解答 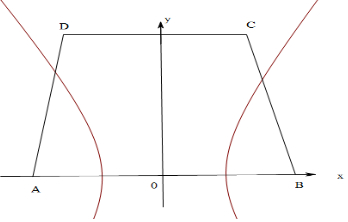 解:以AB为x轴,以AB的中垂线为y轴建立平面坐标系,则B(2,0),C(1,$\sqrt{3}$).
解:以AB为x轴,以AB的中垂线为y轴建立平面坐标系,则B(2,0),C(1,$\sqrt{3}$).
设双曲线的方程为$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1,则a2+b2=c2=4,∴b2=4-a2,
把x=1代入双曲线方程得y2=$\frac{(1-{a}^{2}){b}^{2}}{{a}^{2}}$=$\frac{(1-{a}^{2})(4-{a}^{2})}{{a}^{2}}$=a2-5+$\frac{4}{{a}^{2}}$,
∵双曲线与线段CD(包括端点C、D)有两个交点,
∴a2-5+$\frac{4}{{a}^{2}}$≥3,解得a2≥4+2$\sqrt{3}$(舍)或a2≤4-2$\sqrt{3}$,
∴0<a<$\sqrt{4-2\sqrt{3}}$=$\sqrt{3}-1$,
∴e=$\frac{c}{a}$=$\frac{2}{a}$≥$\frac{2}{\sqrt{3}-1}$=$\sqrt{3}$+1,
故答案为:[$\sqrt{3}$+1,+∞).
点评 本题考查了双曲线的简单性质,属于中档题.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -3 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知抛物线x2=2py和$\frac{{x}^{2}}{2}$-y2=1的公切线PQ(P是PQ与抛物线的切点,未必是PQ与双曲线的切点)与抛物线的准线交于Q,F(0,$\frac{P}{2}$),若$\sqrt{2}$|PQ|=$\sqrt{3}$|PF|,则抛物线的方程是( )
已知抛物线x2=2py和$\frac{{x}^{2}}{2}$-y2=1的公切线PQ(P是PQ与抛物线的切点,未必是PQ与双曲线的切点)与抛物线的准线交于Q,F(0,$\frac{P}{2}$),若$\sqrt{2}$|PQ|=$\sqrt{3}$|PF|,则抛物线的方程是( )| A. | x2=4y | B. | x2=2$\sqrt{3}$y | C. | x2=6y | D. | x2=2$\sqrt{2}$y |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\sqrt{5}$ | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 54种 | B. | 72种 | C. | 120种 | D. | 144种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $-\frac{1}{2}$ | C. | 5 | D. | -5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com