
分析 (Ⅰ) 利用函数的奇偶性转化求解函数的解析式即可.
(Ⅱ) 通过当x=0时,当0<x≤2时,当0<x<1时,求出函数的零点,极值,然后求解实数m的取值范围.
解答 解:(Ⅰ) 当x≤0时,f(x)=(x+2)e-x-2,
当x>0时,则-x<0时,f(-x)=(-x+2)ex-2,
由于f(x)奇函数,则f(x)=-f(-x)=-[(-x+2)ex-2],
故当x>0时,f(x)=(x-2)ex+2.(6分)
(Ⅱ) 当x=0时,f(0)=0.
当0<x≤2时,f(x)=(x-2)ex+2,f'(x)=(x-1)ex,由f'(x)=0,得x=1,
当0<x<1时,f'(x)<0,当1<x<2时,f'(x)>0,则f(x)在(0,1)上单调递减;
在(1,2)上单调递增.则f(x)在x=1处取得极小值f(1)=2-e,(10分)
又f(0)=0,f(2)=2,故当0<x≤2时,f(x)∈[2-e,2].
综上,当x∈[0,2]时,f(x)∈[2-e,2],
所以实数m的取值范围是[2-e,2].(12分)
点评 本题考查函数的导数的应用,函数的单调性以及函数的极值,考查分类讨论思想的应用,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | c>a>b | C. | b>c>a | D. | b>a>c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {a|1<a<2} | B. | {a|-2<a<1} | C. | {a|0<a<2} | D. | {a|0<a<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | c<a<b | C. | c<b<a | D. | b<c<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{3}{4}$,-$\frac{2}{3}$)∪($\frac{2}{3}$,$\frac{3}{4}$] | B. | ($\frac{2}{3}$,$\frac{3}{4}$] | C. | [-$\frac{3}{4}$,-$\frac{1}{2}$)∪($\frac{1}{2}$,$\frac{3}{4}$] | D. | [-$\frac{4}{5}$,-$\frac{3}{4}$)∪($\frac{3}{4}$,$\frac{4}{5}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 经过定点P0(x0,y0)的直线都可以用方程y-y0=k(x-x0)表示 | |
| B. | 经过定点A(0,b)的直线都可以用方程y=kx+b表示 | |
| C. | 不经过原点的直线都可以用方程$\frac{x}{a}$+$\frac{y}{b}$=1表示P1(x1,y1)、P2(x2,y2) | |
| D. | 经过任意两个不同的点的直线都可以用方程(y-y1)(x2-x1)=(x-x1)(y2-y1)来表示 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
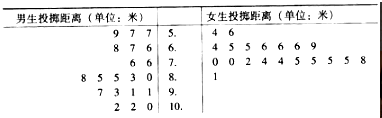
| 男生投掷距离(米) | … | [5.4,6.0) | [6.0,6.6) | [6.6,7.4) | [7.4,7.8) | [7.8,8.6) | [8.6,10.0) | [10.0,+∞) |
| 女生投掷距离(米) | … | [5.1,5.4) | [5.4,5.6) | [5.6,6.4) | [6.4,6.8) | [6.8,7.2) | [7.2,7.6) | [7.6,+∞) |
| 个人得分(分) | … | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com