
已知函数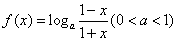 .
.
(1)求函数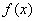 的定义域
的定义域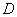 ,并判断
,并判断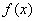 的奇偶性;
的奇偶性;
(2)如果当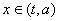 时,
时,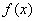 的值域是
的值域是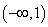 ,求
,求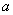 与
与 的值;
的值;
(3)对任意的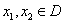 ,是否存在
,是否存在 ,使得
,使得 ,若存在,求出
,若存在,求出 ;若不存在,请说明理由.
;若不存在,请说明理由.
 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
某公司生产某种消防安全产品,年产量x台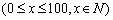 时,销售收入函数
时,销售收入函数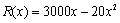 (单位:百元),其成本函数满足
(单位:百元),其成本函数满足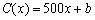 (单位:百元).已知该公司不生产任何产品时,其成本为4000(百元).
(单位:百元).已知该公司不生产任何产品时,其成本为4000(百元).
(1)问该公司生产多少台产品时,利润最大,最大利润是多少?
(2)在经济学中,对于函数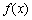 ,我们把函数
,我们把函数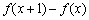 称为函数
称为函数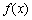 的边际函数,记作
的边际函数,记作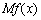 .对于(1)求得的利润函数
.对于(1)求得的利润函数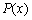 ,求边际函数
,求边际函数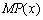 ;并利用边际函数
;并利用边际函数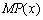 的性质解释公司生产利润情况.(本题所指的函数性质主要包括:函数的单调性、最值、零点等)
的性质解释公司生产利润情况.(本题所指的函数性质主要包括:函数的单调性、最值、零点等)
查看答案和解析>>
科目:高中数学 来源: 题型:
设数列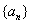 的各项均为正数,前
的各项均为正数,前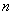 项和为
项和为 ,已知
,已知 .
.
(1)证明数列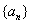 是等差数列,并求其通项公式;
是等差数列,并求其通项公式;
(2)证明:对任意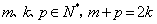 ,都有
,都有 ;
;
(3)对于(2)中的命题,对一般的各项均为正数的等差数列还成立吗?如果成立,请证明你的结论,如果不成立,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知集合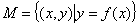 ,若对于任意
,若对于任意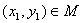 ,存在
,存在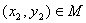 ,使得
,使得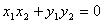 成立,则称集合
成立,则称集合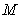 是“
是“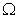 集合”. 给出下列4个集合:
集合”. 给出下列4个集合:
① 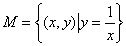 ②
② 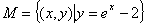
③ 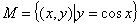 ④
④ 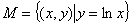
其中所有“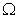 集合”的序号是( )
集合”的序号是( )
A.②③ B.③④ C.①②④ D.①③④.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com