
分析 (I)运用数学归纳法推理论证,
(II)根据递推关系式得出bn=$\frac{{2{b_{n-1}}-1}}{{{b_{n-1}}}}$=2-$\frac{1}{{b}_{n-1}}$,(n∈N*),an-1=2-$\frac{1}{{a}_{n}}$,判断得出b1=$2-\frac{1}{{b}_{1}}$═2-$\frac{1}{{a}_{k}}$=ak-1,…bk=2-$\frac{1}{{b}_{k-1}}$=2$-\frac{1}{{a}_{1}}$=0,可以解决问题.
(III)cn=$\frac{1}{n+1}$推证∴($\frac{1}{n+1}$)${\;}^{\frac{1}{2}}$=$\frac{1}{\sqrt{(n+1)^{3}}}$$<\frac{1}{\sqrt{n(n+1)(n+2)}}$放缩得出($\frac{1}{n+1}$)${\;}^{\frac{1}{2}}$<$\frac{1}{\sqrt{n}}$$-\frac{1}{\sqrt{n+2}}$列出和即可证明.
解答 证明(I)(1)当n=0时,a1=$\frac{1}{2}$,0≤a0<a1<1,
(2)假设n=k(k≥0,k∈N)时,ak<ak+1<1,
则n=k+1时,令f(x)=$\frac{1}{2-x}$,f(x)在(0,1)上单调递增,
∴f(ai)<f(ai+1)<f(1),即ak+1<ak+2<1,
∴n=k+1时命题成立,
综上原命题成立,
(II)∵bn=$\frac{{2{b_{n-1}}-1}}{{{b_{n-1}}}}$=2-$\frac{1}{{b}_{n-1}}$,(n∈N*),an-1=2-$\frac{1}{{a}_{n}}$
∴b1=$2-\frac{1}{{b}_{1}}$═2-$\frac{1}{{a}_{k}}$=ak-1,…bk=2-$\frac{1}{{b}_{k-1}}$=2$-\frac{1}{{a}_{1}}$=0,
∴数列{bn}没有第k+1项及后继项,即数列{bn}是有穷数列.
(III)∵an=$\frac{1}{{2-{a_{n-1}}}}$(n∈N*).∴$\frac{1}{{c}_{n}}$$-\frac{1}{{c}_{n-1}}$=1,
∴cn=$\frac{1}{n+1}$
∴($\frac{1}{n+1}$)${\;}^{\frac{1}{2}}$=$\frac{1}{\sqrt{(n+1)^{3}}}$$<\frac{1}{\sqrt{n(n+1)(n+2)}}$=($\frac{1}{\sqrt{n}}$$-\frac{1}{\sqrt{n+2}}$)$•\frac{1}{\sqrt{n+1}}$$•\frac{\sqrt{n+2}+\sqrt{n}}{2}$<($\frac{1}{\sqrt{n}}$$-\frac{1}{\sqrt{n+2}}$)$•\frac{1}{\sqrt{n+1}}$$•\sqrt{\frac{n+2+n}{2}}$=$\frac{1}{\sqrt{n}}$$-\frac{1}{\sqrt{n+2}}$
∴c${\;}_{1}^{\frac{3}{2}}$+c${\;}_{2}^{\frac{3}{2}}$+…+c${\;}_{n}^{\frac{3}{2}}$<1-$\frac{1}{\sqrt{3}}$$+\frac{1}{\sqrt{2}}$$-\frac{1}{\sqrt{4}}$+…+$\frac{1}{\sqrt{n}}$$-\frac{1}{\sqrt{n+2}}$=1$+\frac{\sqrt{2}}{2}$$-\frac{1}{\sqrt{n+1}}$$-\frac{1}{\sqrt{n+2}}$<1+$\frac{\sqrt{2}}{2}$(n∈N*).
点评 本题综合考查了数列与函数不等式的综合运用,递推关系式的理解运用,放缩法证明不等式,考查了学生的推理论证能力,整体把握问题的能力,难度较大,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
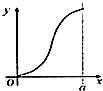 如图,有四个平面图形分别是三角形、平行四边形、直角梯形、圆.垂直于x轴的直线l:x=t(0≤t≤a)经过原点O向右平行移动,l在移动过程中扫过平面图形的面积为y(图中阴影部分),若函数y=f(t)的大致图象如图,那么平面图形的形状不可能是( )
如图,有四个平面图形分别是三角形、平行四边形、直角梯形、圆.垂直于x轴的直线l:x=t(0≤t≤a)经过原点O向右平行移动,l在移动过程中扫过平面图形的面积为y(图中阴影部分),若函数y=f(t)的大致图象如图,那么平面图形的形状不可能是( )| A. | 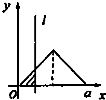 | B. | 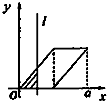 | C. | 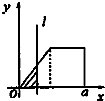 | D. | 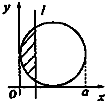 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+y2-8x=0 | B. | y=6x2 | C. | x2+4y2=1 | D. | $\frac{x^2}{9}-\frac{y^2}{4}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com