练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．甲、乙两校各有3名教师报名支教，其中甲校2男1女，乙校1男2女．
    （Ⅰ）若从甲校和乙校报名的教师中各任选1名，求选出的2名教师性别相同的概率；
    （Ⅱ）若从报名的6名教师中任选2名，求选出的2名教师来自同一学校的概率．

    分析 利用列举法确定基本事件的个数，根据古典概型的概率公式，即可得出结论．

    解答 解：（Ⅰ）甲校两名男教师分别用A，B表示，女教师用C表示；乙校男教师用D表示，两名女教师分别用E、F表示．从甲校和乙校的教师中各任选1名的所有可能的结果为：{A，D}，{A，E}，{A，F}，{B，D}，{B，E}，{B，F}，{C，D}，{C，E}，{C，F}，共9种．
    从中选出两名教师性别相同的结果有：{A，D}，{B，D}，{C，E}，{C，F}，共4种，所以选出的两名教师性别相同的概率为$P=\frac{4}{9}$．
    （Ⅱ）从甲校和乙校的教师中任先2名的所有可能的结果为：{A，B}，{A，C}，{A，D}，{A，E}，{A，F}，{B，C}，{B，D}，{B，E}，{B，F}，{C，D}，{C，E}，{C，F}，{D，E}，{D，F}，{E，F}，共15种．从中选出两名教师来自同一学校的结果有：{A，B}，{A，C}，{B，C}，{D，E}，{D，F}，{E，F}，共6种．所以，选出两名教师来自同一学校的概率为$P=\frac{6}{15}=\frac{2}{5}$．

    点评 本题考查古典概型，考查列举法确定基本事件，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    19．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点为F，点B是虚轴上的一个顶点，线段BF与双曲线C的右支交于点A，若$\overrightarrow{BA}$=2$\overrightarrow{AF}$，且|$\overrightarrow{BF}$|=4，则双曲线C的方程为（　　）
    A．$\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{5}$=1B．$\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{12}$=1C．$\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{4}$=1D．$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{6}$=1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知抛物线y2=4x的焦点F，若A，B是该抛物线上的点，∠AFB=90°，线段AB中点M在抛物线的准线上的射影为N，则$\frac{|MN|}{|AB|}$的最大值为     （　　）
    A．$\sqrt{2}$B．1C．$\frac{{\sqrt{2}}}{2}$D．$\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

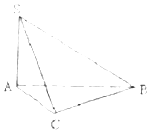    3．在三棱锥S-ABC中，∠SAB=∠SAC=∠ACB=90°，AC=1，BC=$\sqrt{3}，SB=2\sqrt{2}$．
    （1）证明：面SBC⊥面SAC；
    （2）求点A到平面SCB的距离；
    （3）求二面角A-SB-C的平面角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．把函数y=sin（2x+$\frac{π}{6}$）图象上各点的横坐标缩短到原来的$\frac{1}{2}$倍（纵坐标不变），再将图象向右平移$\frac{π}{3}$个单位，得到函数y=g（x），那么g（$\frac{π}{3}$）的值为（　　）
    A．-$\frac{1}{2}$B．$\frac{1}{2}$C．$\frac{\sqrt{3}}{2}$D．-$\frac{\sqrt{3}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．过点（1，1）的抛物线y=ax2的焦点坐标为（　　）
    A．$（{-\frac{1}{4}，0}）$B．$（{0，-\frac{1}{4}}）$C．$（{0，\frac{1}{4}}）$D．$（{\frac{1}{4}，0}）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知数列{an}的前n项和为Sn，且${S_n}+\frac{1}{3}{a_n}=1$（n∈N+）．
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）设bn=log4（1-Sn+1）（n∈N+），${T_n}=\frac{1}{{{b_1}{b_2}}}+\frac{1}{{{b_2}{b_3}}}+…+\frac{1}{{{b_n}{b_{n+1}}}}$，求使${T_n}≥\frac{504}{1009}$成立的最小的正整数n的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．双曲线$C：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的左，右焦点分别是F1（-c，0），F2（c，0），M，N两点在双曲线上，且MN∥F1F2，|F1F2|=3|MN|，线段F1N交双曲线C于点Q，且Q是线段F1N的中点，则双曲线C的离心率为（　　）
    A．3B．$2\sqrt{2}$C．$\frac{{2\sqrt{6}}}{3}$D．$\frac{{\sqrt{5}+1}}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知抛物线C：y2=4x的焦点为F，准线为l，若射线y=2（x-1）（x≤1）与C，l分别交于P、Q两点，则$\frac{|PQ|}{|PF|}$=（　　）
    A．$\sqrt{2}$B．2C．$\sqrt{5}$D．5

    查看答案和解析>>

    同步练习册答案