
| A. | 等腰三角形 | B. | 直角三角形 | ||
| C. | 等边三角形 | D. | 等腰三角形或直角三角形 |
分析 由余弦定理得c2(a2-b2)=(a2-b2)(a2+b2),由C=60°,得到△ABC为等边三角形.
解答 解:∵在△ABC中,acosA=bcosB,
∴由余弦定理得:$a×\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}=b×\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$,
整理,得c2(a2-b2)=(a2-b2)(a2+b2),
∵C=60°,
∴a=b=c,
∴△ABC的形状为等边三角形.
故选:C.
点评 本题考查三角形形状的判断,考查余弦定理、三角形性质等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源:2017届山西临汾一中高三10月月考数学(理)试卷(解析版) 题型:解答题
已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,椭圆
,椭圆 过点
过点 ,直线
,直线 交
交 轴于
轴于 ,且
,且 ,
,  为坐标原点.
为坐标原点.
(1)求椭圆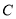 的方程;
的方程;
(2)设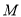 是椭圆
是椭圆 的上顶点,过点
的上顶点,过点 分别作直线
分别作直线 交椭圆
交椭圆 于
于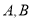 两点,设这两条直线的斜率分别为
两点,设这两条直线的斜率分别为 ,且
,且 ,证明:直线
,证明:直线 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}+1}{2}$ | C. | 2$+\sqrt{2}$ | D. | 1$+\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{8}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 960种 | B. | 984种 | C. | 1080种 | D. | 1440种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com