
 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{1}{2}$,且过点$E({1,\frac{3}{2}})$.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{1}{2}$,且过点$E({1,\frac{3}{2}})$.分析 (1)根据椭圆的离心率公式,求得a=2c,则b2=a2-c2=3c2,将E代入椭圆方程,即可求得a和c的值,即可求得椭圆方程;
(2)设P(x0,y0)(y0≠0),即可得出直线AP的方程,令x=2,即可得到点M的坐标,利用斜率计算公式即可得出k1,k2,再利用点P在椭圆上即可证明.
解答 解:(1)由椭圆的离心率e=$\frac{c}{a}$=$\frac{1}{2}$,则a=2c,则b2=a2-c2=3c2,将E代入椭圆方程:$\frac{1}{4{c}^{2}}+\frac{9}{4×3{c}^{2}}=1$,解得:c=1,
则a=2,b=$\sqrt{3}$,
∴椭圆的标准方程:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
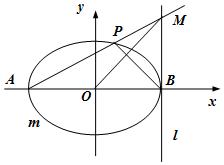
(2)证明:由(1)可知:A(-2,0),B(2,0),设P(x0,y0)(y0≠0),
则直线AP的方程为:y=$\frac{{y}_{0}}{{x}_{0}+2}$(x+2)
令x=2得M(2,$\frac{4{y}_{0}}{{x}_{0}+2}$)
∴k1=$\frac{2{y}_{0}}{{x}_{0}+2}$,则k2=$\frac{{y}_{0}}{{x}_{0}-2}$,
∴k1k2=$\frac{2{y}_{0}^{2}}{{x}_{0}^{2}-4}$,
∵P(x0,y0)在椭圆上,∴$\frac{{x}_{0}^{2}}{4}+\frac{{y}_{0}^{2}}{3}=1$,y02=$\frac{3(4-{x}_{0}^{2})}{4}$
∴k1k2=$\frac{2{y}_{0}^{2}}{{x}_{0}^{2}-4}$=$\frac{3}{2}$为定值.
∴k1k2为定值.
点评 本题考查椭圆的定义及其性质、斜率的计算公式及其直线的点斜式.考查计算能力,属于中档题.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)>g(x) | B. | f(x)<g(x) | C. | f(x)+g(b)>g(x)+f(b) | D. | f(x)+g(a)>g(x)+f(a) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+y-1=0 | B. | x+y+1=0 | C. | x-y+3=0 | D. | x-y-3=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com