练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．已知y=f（x）+2x2是奇函数，且f（1）=2，若g（x）=f（x）+2x，则g（-1）=-8．

    分析 根据函数奇偶性的关系，建立方程关系进行求解即可．

    解答 解：∵y=f（x）+2x2是奇函数，
    ∴设h（x）=f（x）+2x2，则h（-1）=-h（1），
    则f（-1）+2=-[f（1）+2]=-4，
    即f（-1）=-6，
    ∵g（x）=f（x）+2x，
    ∴g（-1）=f（-1）-2=-6-2=-8，
    故答案为：-8

    点评 本题主要考查函数值的计算，根据函数奇偶性的性质进行转化求解是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    7．已知复数z=m2-2m-3+（m-3）i，其中m∈R．
    （1）若m=2，求$\overline{z}$+|z|；
    （2）若z为纯虚数，求实数m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

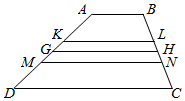    8．如图，四边形ABCD为梯形，其中AB=a，CD=b，若GH表示平行于两底且与它们等距离的线段（即梯形的中位线），KL表示平行于两底且使梯形ABLK与梯形KLCD相似的线段，MN表示平行于两底且将梯形ABCD分为面积相等的两个梯形的线段．
        试研究线段GH，KL，MN与代数式$\frac{a+b}{2}$，$\sqrt{ab}$，$\sqrt{\frac{{a}^{2}+{b}^{2}}{2}}$之间的关系（需写出计算过程），并据此得到它们之间的一个大小关系．请你用基本不等式证明所得的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

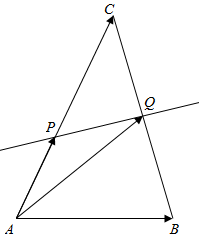    5．如图，已知△ABC的边BC的垂直平分线交AC于点P，交BC于点Q，若|$\overrightarrow{AB}$|=3，|$\overrightarrow{AC}$|=5，则（$\overrightarrow{AP}$+$\overrightarrow{AQ}$）•（$\overrightarrow{AB}$-$\overrightarrow{AC}$）的值为-16．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．某市新批保障性住房建设正在积极筹划中，有关部门已投人3200万购买了-块土地，并计划在这土地上建造一栋n（15＜n＜30）层大楼，每层总面积2000m2．现已知第一层的建筑费用为2200元/m2，并且每升高一层，建筑费用增加80元/m2．
    （1）建设这栋大楼的综合费用为y万元．写出函数y=f（n）的表达式；
    （2）当n为何值时，建设该大楼的每平方米的平均综合费用最低？
    （注：综合费用=建设费用与购地费用之和）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．sin52.5°cos97.5°-sin37.5°sin97.5°=-$\frac{\sqrt{2}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知函数f（x）=cos（sinx）+sin（cosx）．则下列结论正确的是（　　）
    A．f（x）的周期为πB．f（x）在（-$\frac{π}{2}$，0）上单调递减
    C．f（x）的最大值为$\sqrt{2}$D．f（x）的图象关于直线x=π对称

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知圆x2+y2=17在点（1，4）处的切线与幂函数f（x）的图象在点A（1，f（1））处的切线垂直，且不等式$\frac{f（x）}{x}$＞ax2+x在（1，2）上能成立，则实数a的取值范围为（　　）
    A．[0，+∞）B．（$\frac{35}{6}$，+∞）C．（-∞，0]D．（-∞，$\frac{3}{2}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．下列表述正确的是（　　）
    A．过平面β外一点可以作无数条直线与平面β平行
    B．过直线l外一点可作无数条直线平行于l
    C．垂直于两条异面直线的空间直线只有一条
    D．空间三个平面最多把空间分成七部分

    查看答案和解析>>

    同步练习册答案