
| A. | (1,2) | B. | (1,$\sqrt{2}$) | C. | (1,$\sqrt{3}$) | D. | ($\sqrt{2}$,$\sqrt{3}$) |
分析 作出三角形图象,设C=α,则A=2α,根据锐角三角形得出α的取值范围,利用正弦定理求出AC.根据α的范围得出结论.
解答 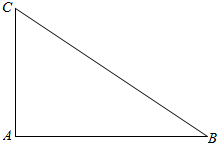 解:设甲救援船位置为A,乙救援船位置为B,呼救信号位置为C,设C=α,则A=2α,B=180°-3α,AB=1.
解:设甲救援船位置为A,乙救援船位置为B,呼救信号位置为C,设C=α,则A=2α,B=180°-3α,AB=1.
∵△ABC是锐角三角形,∴$\left\{\begin{array}{l}{2α<90°}\\{180°-3α<90°}\end{array}\right.$,解得30°<α<45°.
在△ABC中,由正弦定理得$\frac{AB}{sinα}$=$\frac{BC}{sin2α}$,即$\frac{1}{sinα}=\frac{BC}{2sinαcosα}$,∴BC=2cosα.
∵30°<α<45°,∴$\frac{\sqrt{2}}{2}$<cosα<$\frac{\sqrt{3}}{2}$.
∴$\sqrt{2}$<2cosα<$\sqrt{3}$.
故选D.
点评 本题考查了正弦定理,解三角形的实际应用,属于中档题.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
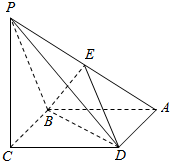 如图所示,已知四棱锥P-ABCD的底面是边长为a的菱形,且∠ABC=120°,PC⊥平面ABCD,PC=a,E为PA的中点.
如图所示,已知四棱锥P-ABCD的底面是边长为a的菱形,且∠ABC=120°,PC⊥平面ABCD,PC=a,E为PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等边三角形 | B. | 等腰直角三角形 | ||
| C. | 直角非等腰三角形 | D. | 等腰非直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com