考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(I)利用导数的运算法则可得:f′(x)=
-=(x>0).对m分类讨论:当m≤0时,当m>0时,即可得出其单调区间.
(II)对于任意x
1∈[
,e],总存在x
2∈[0,
],使得f(x
1)≤g(x
2)成立f(x)
max?≤g(x)
max.利用(I)的结论可得f(x)的最大值,利用二次函数的单调性可得g(x)的最大值.
解答:
解:(I)f′(x)=
-=(x>0).
当m≤0时,f′(x)≤0,此时函数在(0,+∞)单调递减.
当m>0时,由f′(x)=0,解得x=2m.
令f′(x)>0,解得0<x<2m,此时函数f(x)单调递增;令f′(x)<0,解得2m<x,此时函数f(x)单调递减.
∴函数f(x)的单调递增区间为(0,2m),单调递减区间为(2m,+∞).
(II)对于任意x
1∈[
,e],总存在x
2∈[0,
],使得f(x
1)≤g(x
2)成立f(x)
max?≤g(x)
max.
当m=
时,f(x)=
lnx-x,由(I)可知:当x∈
[,1]时,函数f(x)单调递增;
当x∈[1,e]时,函数f(x)单调递减.
∴当x=1时,函数f(x)取得最大值,f(x)
max=f(1)=-
.
当x∈
[0,]时,sinx∈[0,1].
g(x)=2cos
2x+sinx+a=2(1-sin
2x)+sinx+a=-2sin
2x+sinx+2+a=
-2(sinx-)2++a.
∴当sinx=
时,g(x)
max=
g()=
a+.
∴
-≤a+,解得
a≥-.
∴实数a的取值范围是
[-,+∞).
点评:本题考查了利用导数研究函数的单调性极值与最值、二次函数的单调性、恒成立问题的等价转化方法,考查了分类讨论的思想方法,考查了推理能力和计算能力,属于难题.



 名校课堂系列答案
名校课堂系列答案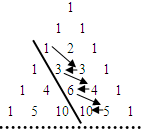 如图,在杨辉三角中,斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数列{an}:1,3,3,4,6,5,10…,记其前n项和为Sn,则S41的值为
如图,在杨辉三角中,斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数列{an}:1,3,3,4,6,5,10…,记其前n项和为Sn,则S41的值为