考点:与二面角有关的立体几何综合题
专题:综合题,空间位置关系与距离,空间角
分析:(1)证明AB1⊥面A1BC,只需证明AB1⊥A1B,CB⊥AB1,证明CB⊥平面AA1B1B,利用四边形A1ABB1为菱形可证;
(2)过B作BD⊥AA1于D,连接CD,证明∠CDB就是二面角C-AA1-B的平面角,求出DB,CD,即可求二面角C-AA1-B的余弦值.
解答:

(1)证明:在△ABC中AC=5,AB=4,BC=3,
所以∠ABC=90°,即CB⊥AB,
又因为四边形BCC
1B
1为矩形,所以CB⊥BB
1,
因为AB∩BB
1=B,
所以CB⊥平面AA
1B
1B,
又因为AB
1?平面AA
1B
1B,
所以CB⊥AB
1,
又因为四边形A
1ABB
1为菱形,
所以AB
1⊥A
1B,
因为CB∩A
1B=B
所以AB
1⊥面A
1BC;
(2)解:过B作BD⊥AA
1于D,连接CD
因为CB⊥平面AA
1B
1B,
所以CB⊥AA
1,
因为CB∩BD=B,
所以AA
1⊥面BCD,
又因为CD?面BCD,
所以AA
1⊥CD,
所以,∠CDB就是二面角C-AA
1-B的平面角.
在直角△ADB中,AB=4,∠DAB=45°,∠ADB=90°,所以DB=2
在直角△CDB中,DB=2
,CB=3,所以CD=
,
所以cos∠CDB=
=
.
点评:本题考查线面垂直的判定,考查面面角,考查学生分析解决问题的能力,正确运用线面垂直的判定,作出面面角是关键.

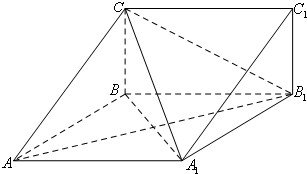 如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=45°,四边形BCC1B1为矩形,若AC=5,AB=4,BC=3
如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=45°,四边形BCC1B1为矩形,若AC=5,AB=4,BC=3 (1)证明:在△ABC中AC=5,AB=4,BC=3,
(1)证明:在△ABC中AC=5,AB=4,BC=3,

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案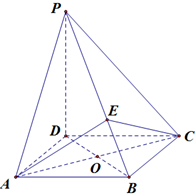 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,AC,BD相交于点O,PD=
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,AC,BD相交于点O,PD= 如图,在四棱锥S-ABCD中,底面ABCD是正方形,四个侧面都是等边三角形,AC与BD的交点为O,E为侧棱SC的中点.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,四个侧面都是等边三角形,AC与BD的交点为O,E为侧棱SC的中点.